- Square :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\multiput(0,0)(4,0){2}{\line(0,1){4}}\multiput(0,0)(0,4){2}{\line(1,0){4}}\put(-0.5,-0.5){\bf D}\put(-0.5,4.2){\bf A}\put(4.2,-0.5){\bf C}\put(4.2,4.2){\bf B}\put(1.5,-0.6){\bf\large x\ cm}\put(4.4,2){\bf\large x\ cm}\end{picture}
- Circle :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\put(0,0){\line(1,0){2.3}}\put(0.5,0.3){\bf\large x\ cm}\end{picture}
- Right angle Triangle :
\setlength{\unitlength}{1cm}\begin{picture}(6,5)\linethickness{.4mm}\put(1,1){\line(1,0){4.5}}\put(1,1){\line(0,1){3.5}}\qbezier(1,4.5)(1,4.5)(5.5,1)\put(.3,2.5){\large\bf a}\put(2.8,.3){\large\bf 2a}\put(1.02,1.02){\framebox(0.3,0.3)}\put(.7,4.8){\large\bf A}\put(.8,.3){\large\bf B}\put(5.8,.3){\large\bf C}\qbezier(4.5,1)(4.3,1.25)(4.6,1.7)\put(3.8,1.3){\large\bf $\Theta$}\end{picture}
- Concentric Circles :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\qbezier(1.2,0)(1.121,1.121)(0,1.2)\qbezier(1.2,0)(1.121,-1.121)(0,-1.2)\qbezier(0,-1.2)(-1.121,-1.121)(-1.2,0)\qbezier(-1.2,0)(-1.121,1.121)(0,1.2)\put(-0,0){\vector(-1,0){2.3}}\put(0,0){\vector(0,1){1.2}}\put(-1.9,0.2){$\bf R_2$}\put(0.2,0.3){$\bf R_1$}\end{picture}
- Rectangle :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\multiput(0,0)(5,0){2}{\line(0,1){3}}\multiput(0,0)(0,3){2}{\line(1,0){5}}\put(0.03,0.02){\framebox(0.25,0.25)}\put(0.03,2.75){\framebox(0.25,0.25)}\put(4.74,2.75){\framebox(0.25,0.25)}\put(4.74,0.02){\framebox(0.25,0.25)}\multiput(2.1,-0.7)(0,4.2){2}{\sf\large x cm}\multiput(-1.4,1.4)(6.8,0){2}{\sf\large y cm}\put(-0.5,-0.4){\bf A}\put(-0.5,3.2){\bf D}\put(5.3,-0.4){\bf B}\put(5.3,3.2){\bf C}\end{picture}
- Triangle :
\setlength{\unitlength}{1 cm}\begin{picture}(0,0)\thicklines\qbezier(1, 0)(1,0)(3,3)\qbezier(5,0)(5,0)(3,3)\qbezier(5,0)(1,0)(1,0)\put(2.85,3.2){$\bf A$}\put(0.5,-0.3){$\bf C$}\put(5.2,-0.3){$\bf B$}\end{picture}
- Distance and Height :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\put(0,0){\line(0,1){6}}\put(0,0){\line(1,0){4}}\put(4,0){\line(0,1){4}}\multiput(0,4)(0.6,0){7}{\qbezier(0,0)(0,0)(0.5,0)}\qbezier(0,6)(0,6)(4,0)\qbezier(0,6)(0,6)(4,4)\put(0,6){\vector(1,0){3}}\qbezier(0.8,6)(1,5.8)(0.6,5.7)\put(1,5.6){$30^{\circ}$}\qbezier(1.8,6)(2.3,5)(1,4.6)\put(2.2,5.2){$60^{\circ}$}\qbezier(3.2,4.42)(3,4.1)(3.25,4)\put(2.4,4.15){$30^{\circ}$}\qbezier(3.3,0)(3.3,0.5)(3.7,0.5)\put(-0.5,-0.5){B}\put(2.7,0.3){$60^{\circ}$}\put(-0.5,6){A}\put(-0.5,3.8){E}\put(-0.5,5){x}\put(4.3,-0.5){D}\put(4.3,3.8){C}\end{picture}
- Rectangle with Diagonal :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\multiput(0,0)(5,0){2}{\line(0,1){3}}\multiput(0,0)(0,3){2}{\line(1,0){5}}\put(0.03,2.74){\framebox(0.25,0.25)}\put(4.74,0.01){\framebox(0.25,0.25)}\put(2,-0.7){\sf\large x cm}\put(-0.5,-0.4){\bf A}\put(-0.5,3.2){\bf D}\put(5.3,-0.4){\bf B}\put(5.3,3.2){\bf C}\qbezier(0,0)(0,0)(5,3)\put(1.65,1.8){\sf\large y cm}\end{picture}
- Square (Alternate method) :
\setlength{\unitlength}{2mm}\begin{picture}(10,10)\linethickness{0.5mm}\put(6,2){\dashbox{0.01}(15,15)}\put(3,0){\bf D}\put(3,18){\bf A}\put(23,18){\bf B}\put(23,0){\bf C}\end{picture}
- Trigonometric Table :
\bullet\:\sf Trigonometric\:Values :\\\\\boxed{\begin{tabular}{c|c|c|c|c|c}Radians/Angle & 0 & 30 & 45 & 60 & 90\\\cline{1-6}Sin \theta & 0 & $\dfrac{1}{2} &$\dfrac{1}{\sqrt{2}} & $\dfrac{\sqrt{3}}{2} & 1\\\cline{1-6}Cos \theta & 1 & $\dfrac{\sqrt{3}}{2}&$\dfrac{1}{\sqrt{2}}&$\dfrac{1}{2}&0\\\cline{1-6}Tan \theta&0&$\dfrac{1}{\sqrt{3}}&1&\sqrt{3}&Not D{e}fined\end{tabular}}
- Cylinder :
\setlength{\unitlength}{1mm}\begin{picture}(5,5)\thicklines\multiput(-0.5,-1)(26,0){2}{\line(0,1){40}}\multiput(12.5,-1)(0,3.2){13}{\line(0,1){1.6}}\multiput(12.5,-1)(0,40){2}{\multiput(0,0)(2,0){7}{\line(1,0){1}}}\multiput(0,0)(0,40){2}{\qbezier(1,0)(12,3)(24,0)\qbezier(1,0)(-2,-1)(1,-2)\qbezier(24,0)(27,-1)(24,-2)\qbezier(1,-2)(12,-5)(24,-2)}\multiput(18,2)(0,32){2}{\sf{r}}\put(9,17.5){\sf{h}}\end{picture}
- Parallelogram :
\setlength{\unitlength}{1 cm}\begin{picture}(0,0)\thicklines\qbezier(1,1)(1,1)(6,1)\put(0.4,0.5){\bf D}\qbezier(1,1)(1,1)(1.6,4)\put(6.2,0.5){\bf C}\qbezier(1.6,4)(1.6,4)(6.6,4)\put(1,4){\bf A}\qbezier(6,1)(6,1)(6.6,4)\put(6.9,3.8){\bf B}\end{picture}
- Parallelogram with diagonals :
\setlength{\unitlength}{1 cm}\begin{picture}(20,15)\thicklines\qbezier(1,1)(1,1)(6,1)\qbezier(1,1)(1,1)(1.6,4)\qbezier(1.6,4)(1.6,4)(6.6,4)\qbezier(6,1)(6,1)(6.6,4)\qbezier(6.6,4)(6.6,4)(1,1)\qbezier(1.6,4)(1.6,4)(6,1)\put(0.7,0.5){\sf A}\put(6,0.5){\sf B}\put(1.4,4.3){\sf D}\put(6.6,4.3){\sf C}\end{picture}
- Trigonometric Identities :
\boxed{\begin{minipage}{6cm} Important Trigonometric identities :- \\ \\ $\: \: 1)\:\sin^2\theta+\cos^2\theta=1 \\ \\ 2)\:\sin^2\theta= 1-\cos^2\theta \\ \\ 3)\:\cos^2\theta=1-\sin^2\theta \\ \\ 4)\:1+\cot^2\theta=\text{cosec}^2 \, \theta \\ \\5)\: \text{cosec}^2 \, \theta-\cot^2\theta =1 \\ \\ 6)\:\text{cosec}^2 \, \theta= 1+\cot^2\theta \\\ \\ 7)\:\sec^2\theta=1+\tan^2\theta \\ \\ 8)\:\sec^2\theta-\tan^2\theta=1 \\ \\ 9)\:\tan^2\theta=\sec^2\theta-1$\end{minipage}}
- Trapezium (1) :
\setlength{\unitlength}{1.2 cm}\begin{picture}(0,0)\linethickness{0.5mm}\qbezier(0,0)(0,0)(1,3)\qbezier(5,0)(5,0)(4,3)\qbezier(1,3)(1,3)(4,3)\qbezier(3,0)(8.2,0)(0,0)\put(-0.5,-0.3){$\sf A$}\put(5.3,-0.3){$\sf B$}\put(4.2,3.1){$\sf C$}\put(0.6,3.1){$\sf D$}\end{picture}
- Algebric Identities :
\boxed{\begin{minipage}{7 cm}\boxed{\bigstar\:\:\textbf{\textsf{Algebric\:Identity}}\:\bigstar}\\\\1)\bf\:(A+B)^{2} = A^{2} + 2AB + B^{2}\\\\2)\sf\: (A-B)^{2} = A^{2} - 2AB + B^{2}\\\\3)\bf\: A^{2} - B^{2} = (A+B)(A-B)\\\\4)\sf\: (A+B)^{2} = (A-B)^{2} + 4AB\\\\5)\bf\: (A-B)^{2} = (A+B)^{2} - 4AB\\\\6)\sf\: (A+B)^{3} = A^{3} + 3AB(A+B) + B^{3}\\\\7)\bf\:(A-B)^{3} = A^{3} - 3AB(A-B) + B^{3}\\\\8)\sf\: A^{3} + B^{3} = (A+B)(A^{2} - AB + B^{2})\\\\\end{minipage}}
- Frequency Table :
\begin{tabular}{|c|c|c|}\cline{1-3}Height (In cm)&No. of Pupil & C.f. \\\cline{1-3}90 - 100 & 5 & 5 \\\cline{1-3}100 - 110 & 2 & 7\\\cline{1-3}110 - 120 & 3 & 10\\\cline{1-3}120 - 130 & 8 & 18\\\cline{1-3}130 - 140 & 8 & 26\\\cline{1-3}140 - 150 & 6 & 32\\\cline{1-3}&\sum\limits f=32&\\\cline{1-3}\end{tabular}
- Trigonometric Full Table :
\Large{ \begin{tabular}{|c|c|c|c|c|c|} \cline{1-6} \theta & \sf 0^{\circ} & \sf 30^{\circ} & \sf 45^{\circ} & \sf 60^{\circ} & \sf 90^{\circ} \\ \cline{1-6} $ \sin $ & 0 & $\dfrac{1}{2 }$ & $\dfrac{1}{ \sqrt{2} }$ & $\dfrac{ \sqrt{3}}{2}$ & 1 \\ \cline{1-6} $ \cos $ & 1 & $ \dfrac{ \sqrt{ 3 }}{2} } $ & $ \dfrac{1}{ \sqrt{2} } $ & $ \dfrac{ 1 }{ 2 } $ & 0 \\ \cline{1-6} $ \tan $ & 0 & $ \dfrac{1}{ \sqrt{3} } $ & 1 & $ \sqrt{3} $ & $ \infty $ \\ \cline{1-6} \cot & $ \infty $ &$ \sqrt{3} $ & 1 & $ \dfrac{1}{ \sqrt{3} } $ &0 \\ \cline{1 - 6} \sec & 1 & $ \dfrac{2}{ \sqrt{3}} $ & $ \sqrt{2} $ & 2 & $ \infty $ \\ \cline{1-6} \csc & $ \infty $ & 2 & $ \sqrt{2 } $ & $ \dfrac{ 2 }{ \sqrt{ 3 } } $ & 1 \\ \cline{1 - 6}\end{tabular}}
- Cuboid :
\setlength{\unitlength}{0.74 cm}\begin{picture}\thicklines\put(5.6,5.4){\bf A}\put(11.1,5.4){\bf B}\put(11.2,9){\bf C}\put(5.3,8.6){\bf D}\put(3.3,10.2){\bf E}\put(3.3,7){\bf F}\put(9.25,10.35){\bf H}\put(9.35,7.35){\bf G}\put(3.5,6.1){\sf x\:cm}\put(7.7,6.3){\sf y\:cm}\put(11.3,7.45){\sf z\:cm}\put(6,6){\line(1,0){5}}\put(6,9){\line(1,0){5}}\put(11,9){\line(0,-1){3}}\put(6,6){\line(0,1){3}}\put(4,7.3){\line(1,0){5}}\put(4,10.3){\line(1,0){5}}\put(9,10.3){\line(0,-1){3}}\put(4,7.3){\line(0,1){3}}\put(6,6){\line(-3,2){2}}\put(6,9){\line(-3,2){2}}\put(11,9){\line(-3,2){2}}\put(11,6){\line(-3,2){2}}\end{picture}
- Cone :
\setlength{\unitlength}{1.2mm}\begin{picture}(5,5)\thicklines\put(0,0){\qbezier(1,0)(12,3)(24,0)\qbezier(1,0)(-2,-1)(1,-2)\qbezier(24,0)(27,-1)(24,-2)\qbezier(1,-2)(12,-5)(24,-2)}\put(-0.5,-1){\line(1,2){13}}\put(25.5,-1){\line(-1,2){13}}\multiput(12.5,-1)(2,0){7}{\line(1,0){1}}\multiput(12.5,-1)(0,4){7}{\line(0,1){2}}\put(18,1.6){\sf{r}}\put(9.5,10){\sf{h}}\end{picture}
- Cube :
\setlength{\unitlength}{4mm}\begin{picture}(10,6)\thicklines\put(0,1){\line(0,1){10}}\put(0,1){\line(1,0){10}}\put(10,1){\line(0,1){10}}\put(0,11){\line(1,0){10}}\put(0,11){\line(1,1){5}}\put(10,11){\line(1,1){5}}\put(10,1){\line(1,1){5}}\put(0,1){\line(1,1){5}}\put(5,6){\line(1,0){10}}\put(5,6){\line(0,1){10}}\put(5,16){\line(1,0){10}}\put(15,6){\line(0,1){10}}\put(4.6,-0.5){\bf\large y m}\put(13.5,3){\bf\large z m}\put(-4,5.8){\bf\large x m}\end{picture}
- LCM :
\Large{ \begin{array}{c|c} \tt 2 & \sf{ 48 , 72 , 100} \\ \cline{1-2} \tt 2 & \sf { 24 , 36 , 50} \\ \cline{1-2} \tt 2 & \sf{ 12 , 18 , 25} \\ \cline{1-2} \tt 2 & \sf{ 6 , 9 , 25} \\ \cline{1-2} \tt 3 & \sf{ 3 , 9 , 25 }\\ \cline{1-2} \tt 3 & \sf{ 1 , 3 , 25 }\\ \cline{1-2} \tt 5 & \sf{ 1, 1 , 25} \\ \cline{1-2} \tt 5 & \sf{ 1 , 1, 5 }\\ \cline{1-2} & \sf{ 1 , 1 , 1} \end{array}}
- Division :
\sf\Large\qquad\quad16\\ \begin{array}{cc} \cline{2 - 2}\sf 20 )&\sf \ 327\\&\sf - 20 \downarrow\\ \cline{2-2}& \sf \ \ \ \ 127\\ &\sf \ - 120 \\ \cline{2-2} & \sf \ \007 \\ \cline{2-2} \end{array}\\\\\\ Divisor \rightarrow 20 \\ \\ Quotient \rightarrow 16\\\\Remainder \rightarrow 7
- Circle-Triangle combination (1) :
\setlength{\unitlength}{1.1mm}\begin{picture}(50,55)\thicklines\qbezier(25.000,10.000)(33.284,10.000)(39.142,15.858)\qbezier(39.142,15.858)(45.000,21.716)(45.000,30.000)\qbezier(45.000,30.000)(45.000,38.284)(39.142,44.142)\qbezier(39.142,44.142)(33.284,50.000)(25.000,50.000)\qbezier(25.000,50.000)(16.716,50.000)(10.858,44.142)\qbezier(10.858,44.142)( 5.000,38.284)( 5.000,30.000)\qbezier( 5.000,30.000)( 5.000,21.716)(10.858,15.858)\qbezier(10.858,15.858)(16.716,10.000)(25.000,10.000)\put(25,30){\line(1,1){14}}\put(25,30){\line(1, - 1){14}}\put(39,15.8){\line(3,1){42}}\put(39,44.2){\line(3, - 1){42}}\put(39,16){\line(0,1){28}}\put(25,30){\circle*{1}}\put(81,30){\circle*{1}}\put(22,30){\sf O}\put(40,46){\sf A}\put(40,12){\sf B}\put(83,30){\sf P}\end{picture}
- Circle-Triangle combination (2) :
\setlength{\unitlength}{1.2mm}\begin{picture}(50,55)\thicklines\qbezier(25.000,10.000)(33.284,10.000)(39.142,15.858)\qbezier(39.142,15.858)(45.000,21.716)(45.000,30.000)\qbezier(45.000,30.000)(45.000,38.284)(39.142,44.142)\qbezier(39.142,44.142)(33.284,50.000)(25.000,50.000)\qbezier(25.000,50.000)(16.716,50.000)(10.858,44.142)\qbezier(10.858,44.142)( 5.000,38.284)( 5.000,30.000)\qbezier( 5.000,30.000)( 5.000,21.716)(10.858,15.858)\qbezier(10.858,15.858)(16.716,10.000)(25.000,10.000)\put(25,30){\line(5, - 4){16}}\put(25,30){\circle*{1}}\put(24,32){\sf\large{O}}\put(25,30){\line(0, - 5){13}}\put(6,14){\sf\large{A}}\put(25,30){\line(- 5, - 4){16}}\put(10,17){\line(5, 0){30}}\put(42,14){\sf\large{B}}\put(24,13){\sf\large{C}}\end{picture}
- Trapezium (2) :
\setlength{\unitlength}{1.5cm}\begin{picture}\thicklines\qbezier(0,0)(0,0)(1,2.2)\qbezier(0,0)(0,0)(4,0)\qbezier(3,2.2)(4,0)(4,0)\qbezier(1.5,2.2)(0,2.2)(3,2.2)\put(0.8,2.4){$\bf A $}\put(3,2.4){$\bf D $}\put(-0.3,-0.3){$\bf B$}\put(4,-0.3){$\bf C$}\put(4.4,0){\vector(0,0){2.2}}\put( 4.4, 0){\vector(0,-1){0.1}}\put(4.6,1){$\bf y\ cm$}\put(0, -0.5){\vector(1,0){4}}\put(0, -0.5){\vector( - 1, 0){0.1}}\put(1.7, - 0.9){$\bf z\ cm $}\put(0.8, 2.8){\vector(1,0){2.5}}\put(0.8, 2.8){\vector( - 1, 0){0.1}}\put(1.7, 3){$\bf x\ cm $}\end{picture}
• Sector :
\setlength{\unitlength}{1.2mm}\begin{picture}\thicklines\qbezier(25.000,10.000)(33.284,10.000)(39.142,15.858)\qbezier(39.142,15.858)(45.000,21.716)(45.000,30.000)\qbezier(45.000,30.000)(45.000,38.284)(39.142,44.142)\qbezier(39.142,44.142)(33.284,50.000)(25.000,50.000)\qbezier(25.000,50.000)(16.716,50.000)(10.858,44.142)\qbezier(10.858,44.142)( 5.000,38.284)( 5.000,30.000)\qbezier( 5.000,30.000)( 5.000,21.716)(10.858,15.858)\qbezier(10.858,15.858)(16.716,10.000)(25.000,10.000)\put(25,30){\line(5, - 4){16}}\put(25,30){\circle*{1}}\put(24,32){\sf\large{O}}\put(15,40){\sf\large{Major Sector}}\put(5,14){\sf\large{A}}\put(25,30){\line(- 5, -4){16}}\put(43,14){\sf\large{B}}\put(14,16){\sf\large{Minor Sector}}\end{picture}
- Tangent to a circle from a point :
\setlength{\unitlength}{1.1mm}\begin{picture}(50,55)\thicklines\qbezier(25.000,10.000)(33.284,10.000)(39.142,15.858)\qbezier(39.142,15.858)(45.000,21.716)(45.000,30.000)\qbezier(45.000,30.000)(45.000,38.284)(39.142,44.142)\qbezier(39.142,44.142)(33.284,50.000)(25.000,50.000)\qbezier(25.000,50.000)(16.716,50.000)(10.858,44.142)\qbezier(10.858,44.142)( 5.000,38.284)( 5.000,30.000)\qbezier( 5.000,30.000)( 5.000,21.716)(10.858,15.858)\qbezier(10.858,15.858)(16.716,10.000)(25.000,10.000)\put(25,30){\line(1,3){6.4}}\put(25,30){\line(1, - 3){6.4}}\put(20,7){\line(3,1){68.5}}\put(20,52.8){\line(3, - 1){68.5}}\put(25,30){\circle*{1}}\put(88,30){\circle*{1.2}}\put(22,30){\sf O}\put(31,6){\sf A}\put(31,52){\sf B}\put(90,28.5){\sf P}\multiput(25,30)(3,0){21}{\line(2,0){1.8}}\qbezier(81.5,32)(78,30)(81,27.5)\qbezier(76,30)(74.5,28)(76,26)\put(33,45){\line(1,3){1.1}}\put(30,45.8){\line(3, - 1){3.2}}\put(30.5,14){\line(3,1){3.2}}\put(33.5,15){\line(1, - 3){1.1}}\put(21,18){\sf 6 cm}\put(73,30.8){\sf 120^\circ$}\put(69,26){\sf 60^\circ$}\end{picture}
- Parallelogram related :
\setlength{\unitlength}{1 cm}\begin{picture}(20,15)\thicklines\qbezier(1,1)(1,1)(6,1)\qbezier(1,1)(1,1)(2,4)\qbezier(2,4)(1.6,4)(7,4)\qbezier(6,1)(6,1)(7,4)\qbezier(2,4)(2,4)(2,1)\qbezier(2,4)(1.6,4)(6.5,2.5)\put(0.7,0.5){\sf B}\put(6,0.5){\sf C}\put(1.8,4.3){\sf A}\put(7,4.3){\sf D}\put(2,0.5){\sf N}\put(3.3,0.5){\sf x cm}\put(6.7,1.5){\sf y cm}\put(6.8,2.4){\sf M}\put(2.2,2.2){\sf z cm}\end{picture}
- Cyclic quadrilateral :
\setlength{\unitlength}{1.5cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\put(-1.58,1.7){\line(1,0){3.15}}\put(-1.9,-1.3){\line(1,0){3.8}}\qbezier(-1.58,1.7)(-1.58,1.7)(-1.9,-1.3)\qbezier(1.57,1.7)(1.57,1.7)(1.9,-1.3)\qbezier(-1.45,-1.3)(-1.4,-0.9)(-1.85,-0.85)\put(-1.4,-0.9){$\bf\large X^{\circ}$}\end{picture}
- Math code :
\setlength{\unitlength}{0.8cm}\begin{picture}(0,0)\thicklines\qbezier(0.2,0)(0.3,2)(2,2)\qbezier(2,2)(3.7,2)(3.8,0)\put(0.2,0){\line(-1,0){3}}\multiput(-2.8,0)(6.6,0){2}{\line(0,-1){3}}\put(-2.8,-3){\line(1,0){6.6}}\put(-2.78,-3){\framebox(0.5,0.5)}\put(0,0.3){\vector(-1,0){2.8}}\put(0,0.3){\vector(1,0){0.1}}\put(-2.8,-3.3){\vector(1,0){6.6}}\put(-2.8,-3.3){\vector(-1,0){0.1}}\put(-3.2,-3){\vector(0,1){3}}\put(-3.2,-3){\vector(0,-2){0.1}}\put(-1.5,0.5){\bf x}\put(0,-4){\bf z}\put(-3.8,-1.6){\bf y}\end{picture}
- Math Code :
\setlength{\unitlength}{1.2cm}\begin{picture}(0,0)\thicklines\qbezier(0,2)(-1.7,1.7)(-1.8,0)\qbezier(-1.8,0)(-1.7,-1.7)(0,-2)\qbezier(0,2)(0,2)(4,0)\qbezier(0,-2)(0,-2)(4,0)\multiput(0,2)(0,-0.29){14}{\line(0,-1){0.18}}\multiput(0,0)(0.31,0){13}{\line(1,0){0.18}}\put(0.2,-0.2){\vector(1,0){3.8}}\put(0.2,-0.2){\vector(-1,0){0.1}}\put(1.6,-0.5){\bf y}\linethickness{0.3mm}\qbezier(4,0.2)(4,0.2)(0.1,2.2)\put(4,0.2){\vector(3,-2){0.1}}\put(0.1,2.2){\vector(-3,2){0.1}}\put(2,1.4){\bf x}\put(-0.5,-0.1){\bf O}\put(4.5,-0.1){\bf P}\end{picture}
- Math Code :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\qbezier(-3,1.5)(0,0)(3,1.5)\qbezier(-3,1.5)(-2.5,4)(0,4.2)\qbezier(3,1.5)(2.5,4)(0,4.2)\put(-3.5,-4.3){\framebox(6,5)}\qbezier(-3.5,0.7)(-3.5,0.7)(-3,1.5)\multiput(2.5,-4.3)(0,5){2}{\line(2,3){1.5}}\put(4,-2.05){\line(0,1){5}}\put(4,2.95){\line(-1,0){1.5}}\multiput(-3,1.5)(0.3,0){20}{\line(1,0){0.2}}\put(-0.5,2){\bf x\ cm}\put(-3.3,0){\vector(1,0){5.7}}\put(-3.3,0){\vector(-1,0){0.1}}\put(-0.9,-0.6){\bf x\ cm}\end{picture}
- Formulas related to SA & Volume :
\begin{array}{|c|c|c|}\cline{1-3}\bf Shape&\bf Volume\ formula&\bf Surface\ area formula\\\cline{1-3}\sf Cube&\tt l^3}&\tt 6l^2\\\cline{1-3}\sf Cuboid&\tt lbh&\tt 2(lb+bh+lh)\\\cline{1-3}\sf Cylinder&\tt {\pi}r^2h&\tt 2\pi{r}(r+h)\\\cline{1-3}\sf Hollow\ cylinder&\tt \pi{h}(R^2-r^2)&\tt 2\pi{rh}+2\pi{Rh}+2\pi(R^2-r^2)\\\cline{1-3}\sf Cone&\tt 1/3\ \pi{r^2}h&\tt \pi{r}(r+s)\\\cline{1-3}\sf Sphere&\tt 4/3\ \pi{r}^3&\tt 4\pi{r}^2\\\cline{1-3}\sf Hemisphere&\tt 2/3\ \pi{r^3}&\tt 3\pi{r}^2\\\cline{1-3}\end{array}
- Random code :
\setlength{\unitlength}{1.2 cm}\begin{picture}(0,0)\linethickness{0.4mm}\qbezier(0,0)(0,0)(1,3)\qbezier(4.6,1)(4.6,1)(4,3)\qbezier(1,3)(1,3)(4,3)\qbezier(4.6,1)(4.6,1)(0,0)\qbezier(4,3)(4,3)(0,0)\qbezier(4.6,1)(4.6,1)(3,2.25)\qbezier(2,1.5)(2,1.5)(1,3)\qbezier(2.2,1.7)(2.2,1.7)(2.05,1.9)\qbezier(2.05,1.9)(2.05,1.9)(1.82,1.74)\qbezier(3.25,2.4)(3.25,2.4)(3.44,2.25)\qbezier(3.44,2.25)(3.44,2.25)(3.25,2.05)\put(-0.4,-0.5){\sf C}\put(4.8,0.6){\sf B}\put(4.2,3.2){\sf A}\put(0.4,3){\sf D}\end{picture}
- Law's of exponents :
\begin{gathered}\boxed{\begin{minipage}{5 cm}\bf{\dag}\:\:\underline{\text{Law of Exponents :}}\\\\\bigstar\:\:\sf\dfrac{a^m}{a^n} = a^{m - n}\\\\\bigstar\:\:\sf{(a^m)^n = a^{mn}}\\\\\bigstar\:\:\sf(a^m)(a^n) = a^{m + n}\\\\\bigstar\:\:\sf\dfrac{1}{a^n} = a^{-n}\\\\\bigstar\:\:\sf\sqrt[\sf n]{\sf a} = (a)^{\dfrac{1}{n}}\end{minipage}}\end{gathered
- Circle with diameter :
\setlength{\unitlength}{1mm}\begin{picture}(50,55)\linethickness{0.4mm}\qbezier(45,30)(45,30)(5,30)\qbezier(25.000,10.000)(33.284,10.000)(39.142,15.858)\qbezier(39.142,15.858)(45.000,21.716)(45.000,30.000)\qbezier(45.000,30.000)(45.000,38.284)(39.142,44.142)\qbezier(39.142,44.142)(33.284,50.000)(25.000,50.000)\qbezier(25.000,50.000)(16.716,50.000)(10.858,44.142)\qbezier(10.858,44.142)( 5.000,38.284)( 5.000,30.000)\qbezier( 5.000,30.000)( 5.000,21.716)(10.858,15.858)\qbezier(10.858,15.858)(16.716,10.000)(25.000,10.000)\multiput(5,30)(20,0){3}{\circle*{1}}\end{picture}
- Circle :
- Right angle Triangle :
- Concentric Circles :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\qbezier(1.2,0)(1.121,1.121)(0,1.2)\qbezier(1.2,0)(1.121,-1.121)(0,-1.2)\qbezier(0,-1.2)(-1.121,-1.121)(-1.2,0)\qbezier(-1.2,0)(-1.121,1.121)(0,1.2)\put(-0,0){\vector(-1,0){2.3}}\put(0,0){\vector(0,1){1.2}}\put(-1.9,0.2){$\bf R_2$}\put(0.2,0.3){$\bf R_1$}\end{picture}
- Rectangle :
- Triangle :
- Distance and Height :
- Rectangle with Diagonal :
- Square (Alternate method) :
- Trigonometric Table :
- Cylinder :
\setlength{\unitlength}{1mm}\begin{picture}(5,5)\thicklines\multiput(-0.5,-1)(26,0){2}{\line(0,1){40}}\multiput(12.5,-1)(0,3.2){13}{\line(0,1){1.6}}\multiput(12.5,-1)(0,40){2}{\multiput(0,0)(2,0){7}{\line(1,0){1}}}\multiput(0,0)(0,40){2}{\qbezier(1,0)(12,3)(24,0)\qbezier(1,0)(-2,-1)(1,-2)\qbezier(24,0)(27,-1)(24,-2)\qbezier(1,-2)(12,-5)(24,-2)}\multiput(18,2)(0,32){2}{\sf{r}}\put(9,17.5){\sf{h}}\end{picture}
- Parallelogram :
\setlength{\unitlength}{1 cm}\begin{picture}(0,0)\thicklines\qbezier(1,1)(1,1)(6,1)\put(0.4,0.5){\bf D}\qbezier(1,1)(1,1)(1.6,4)\put(6.2,0.5){\bf C}\qbezier(1.6,4)(1.6,4)(6.6,4)\put(1,4){\bf A}\qbezier(6,1)(6,1)(6.6,4)\put(6.9,3.8){\bf B}\end{picture}
- Parallelogram with diagonals :
\setlength{\unitlength}{1 cm}\begin{picture}(20,15)\thicklines\qbezier(1,1)(1,1)(6,1)\qbezier(1,1)(1,1)(1.6,4)\qbezier(1.6,4)(1.6,4)(6.6,4)\qbezier(6,1)(6,1)(6.6,4)\qbezier(6.6,4)(6.6,4)(1,1)\qbezier(1.6,4)(1.6,4)(6,1)\put(0.7,0.5){\sf A}\put(6,0.5){\sf B}\put(1.4,4.3){\sf D}\put(6.6,4.3){\sf C}\end{picture}
- Trigonometric Identities :
\boxed{\begin{minipage}{6cm} Important Trigonometric identities :- \\ \\ $\: \: 1)\:\sin^2\theta+\cos^2\theta=1 \\ \\ 2)\:\sin^2\theta= 1-\cos^2\theta \\ \\ 3)\:\cos^2\theta=1-\sin^2\theta \\ \\ 4)\:1+\cot^2\theta=\text{cosec}^2 \, \theta \\ \\5)\: \text{cosec}^2 \, \theta-\cot^2\theta =1 \\ \\ 6)\:\text{cosec}^2 \, \theta= 1+\cot^2\theta \\\ \\ 7)\:\sec^2\theta=1+\tan^2\theta \\ \\ 8)\:\sec^2\theta-\tan^2\theta=1 \\ \\ 9)\:\tan^2\theta=\sec^2\theta-1$\end{minipage}}
- Trapezium (1) :
\setlength{\unitlength}{1.2 cm}\begin{picture}(0,0)\linethickness{0.5mm}\qbezier(0,0)(0,0)(1,3)\qbezier(5,0)(5,0)(4,3)\qbezier(1,3)(1,3)(4,3)\qbezier(3,0)(8.2,0)(0,0)\put(-0.5,-0.3){$\sf A$}\put(5.3,-0.3){$\sf B$}\put(4.2,3.1){$\sf C$}\put(0.6,3.1){$\sf D$}\end{picture}
- Algebric Identities :
\boxed{\begin{minipage}{7 cm}\boxed{\bigstar\:\:\textbf{\textsf{Algebric\:Identity}}\:\bigstar}\\\\1)\bf\:(A+B)^{2} = A^{2} + 2AB + B^{2}\\\\2)\sf\: (A-B)^{2} = A^{2} - 2AB + B^{2}\\\\3)\bf\: A^{2} - B^{2} = (A+B)(A-B)\\\\4)\sf\: (A+B)^{2} = (A-B)^{2} + 4AB\\\\5)\bf\: (A-B)^{2} = (A+B)^{2} - 4AB\\\\6)\sf\: (A+B)^{3} = A^{3} + 3AB(A+B) + B^{3}\\\\7)\bf\:(A-B)^{3} = A^{3} - 3AB(A-B) + B^{3}\\\\8)\sf\: A^{3} + B^{3} = (A+B)(A^{2} - AB + B^{2})\\\\\end{minipage}}
- Frequency Table :
\begin{tabular}{|c|c|c|}\cline{1-3}Height (In cm)&No. of Pupil & C.f. \\\cline{1-3}90 - 100 & 5 & 5 \\\cline{1-3}100 - 110 & 2 & 7\\\cline{1-3}110 - 120 & 3 & 10\\\cline{1-3}120 - 130 & 8 & 18\\\cline{1-3}130 - 140 & 8 & 26\\\cline{1-3}140 - 150 & 6 & 32\\\cline{1-3}&\sum\limits f=32&\\\cline{1-3}\end{tabular}
- Trigonometric Full Table :
- Cuboid :
\setlength{\unitlength}{0.74 cm}\begin{picture}\thicklines\put(5.6,5.4){\bf A}\put(11.1,5.4){\bf B}\put(11.2,9){\bf C}\put(5.3,8.6){\bf D}\put(3.3,10.2){\bf E}\put(3.3,7){\bf F}\put(9.25,10.35){\bf H}\put(9.35,7.35){\bf G}\put(3.5,6.1){\sf x\:cm}\put(7.7,6.3){\sf y\:cm}\put(11.3,7.45){\sf z\:cm}\put(6,6){\line(1,0){5}}\put(6,9){\line(1,0){5}}\put(11,9){\line(0,-1){3}}\put(6,6){\line(0,1){3}}\put(4,7.3){\line(1,0){5}}\put(4,10.3){\line(1,0){5}}\put(9,10.3){\line(0,-1){3}}\put(4,7.3){\line(0,1){3}}\put(6,6){\line(-3,2){2}}\put(6,9){\line(-3,2){2}}\put(11,9){\line(-3,2){2}}\put(11,6){\line(-3,2){2}}\end{picture}
- Cone :
\setlength{\unitlength}{1.2mm}\begin{picture}(5,5)\thicklines\put(0,0){\qbezier(1,0)(12,3)(24,0)\qbezier(1,0)(-2,-1)(1,-2)\qbezier(24,0)(27,-1)(24,-2)\qbezier(1,-2)(12,-5)(24,-2)}\put(-0.5,-1){\line(1,2){13}}\put(25.5,-1){\line(-1,2){13}}\multiput(12.5,-1)(2,0){7}{\line(1,0){1}}\multiput(12.5,-1)(0,4){7}{\line(0,1){2}}\put(18,1.6){\sf{r}}\put(9.5,10){\sf{h}}\end{picture}
- Cube :
\setlength{\unitlength}{4mm}\begin{picture}(10,6)\thicklines\put(0,1){\line(0,1){10}}\put(0,1){\line(1,0){10}}\put(10,1){\line(0,1){10}}\put(0,11){\line(1,0){10}}\put(0,11){\line(1,1){5}}\put(10,11){\line(1,1){5}}\put(10,1){\line(1,1){5}}\put(0,1){\line(1,1){5}}\put(5,6){\line(1,0){10}}\put(5,6){\line(0,1){10}}\put(5,16){\line(1,0){10}}\put(15,6){\line(0,1){10}}\put(4.6,-0.5){\bf\large y m}\put(13.5,3){\bf\large z m}\put(-4,5.8){\bf\large x m}\end{picture}
- LCM :
\Large{ \begin{array}{c|c} \tt 2 & \sf{ 48 , 72 , 100} \\ \cline{1-2} \tt 2 & \sf { 24 , 36 , 50} \\ \cline{1-2} \tt 2 & \sf{ 12 , 18 , 25} \\ \cline{1-2} \tt 2 & \sf{ 6 , 9 , 25} \\ \cline{1-2} \tt 3 & \sf{ 3 , 9 , 25 }\\ \cline{1-2} \tt 3 & \sf{ 1 , 3 , 25 }\\ \cline{1-2} \tt 5 & \sf{ 1, 1 , 25} \\ \cline{1-2} \tt 5 & \sf{ 1 , 1, 5 }\\ \cline{1-2} & \sf{ 1 , 1 , 1} \end{array}}
- Division :
\sf\Large\qquad\quad16\\ \begin{array}{cc} \cline{2 - 2}\sf 20 )&\sf \ 327\\&\sf - 20 \downarrow\\ \cline{2-2}& \sf \ \ \ \ 127\\ &\sf \ - 120 \\ \cline{2-2} & \sf \ \007 \\ \cline{2-2} \end{array}\\\\\\ Divisor \rightarrow 20 \\ \\ Quotient \rightarrow 16\\\\Remainder \rightarrow 7
- Circle-Triangle combination (1) :
\setlength{\unitlength}{1.1mm}\begin{picture}(50,55)\thicklines\qbezier(25.000,10.000)(33.284,10.000)(39.142,15.858)\qbezier(39.142,15.858)(45.000,21.716)(45.000,30.000)\qbezier(45.000,30.000)(45.000,38.284)(39.142,44.142)\qbezier(39.142,44.142)(33.284,50.000)(25.000,50.000)\qbezier(25.000,50.000)(16.716,50.000)(10.858,44.142)\qbezier(10.858,44.142)( 5.000,38.284)( 5.000,30.000)\qbezier( 5.000,30.000)( 5.000,21.716)(10.858,15.858)\qbezier(10.858,15.858)(16.716,10.000)(25.000,10.000)\put(25,30){\line(1,1){14}}\put(25,30){\line(1, - 1){14}}\put(39,15.8){\line(3,1){42}}\put(39,44.2){\line(3, - 1){42}}\put(39,16){\line(0,1){28}}\put(25,30){\circle*{1}}\put(81,30){\circle*{1}}\put(22,30){\sf O}\put(40,46){\sf A}\put(40,12){\sf B}\put(83,30){\sf P}\end{picture}
- Circle-Triangle combination (2) :
\setlength{\unitlength}{1.2mm}\begin{picture}(50,55)\thicklines\qbezier(25.000,10.000)(33.284,10.000)(39.142,15.858)\qbezier(39.142,15.858)(45.000,21.716)(45.000,30.000)\qbezier(45.000,30.000)(45.000,38.284)(39.142,44.142)\qbezier(39.142,44.142)(33.284,50.000)(25.000,50.000)\qbezier(25.000,50.000)(16.716,50.000)(10.858,44.142)\qbezier(10.858,44.142)( 5.000,38.284)( 5.000,30.000)\qbezier( 5.000,30.000)( 5.000,21.716)(10.858,15.858)\qbezier(10.858,15.858)(16.716,10.000)(25.000,10.000)\put(25,30){\line(5, - 4){16}}\put(25,30){\circle*{1}}\put(24,32){\sf\large{O}}\put(25,30){\line(0, - 5){13}}\put(6,14){\sf\large{A}}\put(25,30){\line(- 5, - 4){16}}\put(10,17){\line(5, 0){30}}\put(42,14){\sf\large{B}}\put(24,13){\sf\large{C}}\end{picture}
- Trapezium (2) :
\setlength{\unitlength}{1.5cm}\begin{picture}\thicklines\qbezier(0,0)(0,0)(1,2.2)\qbezier(0,0)(0,0)(4,0)\qbezier(3,2.2)(4,0)(4,0)\qbezier(1.5,2.2)(0,2.2)(3,2.2)\put(0.8,2.4){$\bf A $}\put(3,2.4){$\bf D $}\put(-0.3,-0.3){$\bf B$}\put(4,-0.3){$\bf C$}\put(4.4,0){\vector(0,0){2.2}}\put( 4.4, 0){\vector(0,-1){0.1}}\put(4.6,1){$\bf y\ cm$}\put(0, -0.5){\vector(1,0){4}}\put(0, -0.5){\vector( - 1, 0){0.1}}\put(1.7, - 0.9){$\bf z\ cm $}\put(0.8, 2.8){\vector(1,0){2.5}}\put(0.8, 2.8){\vector( - 1, 0){0.1}}\put(1.7, 3){$\bf x\ cm $}\end{picture}
\setlength{\unitlength}{1.2mm}\begin{picture}\thicklines\qbezier(25.000,10.000)(33.284,10.000)(39.142,15.858)\qbezier(39.142,15.858)(45.000,21.716)(45.000,30.000)\qbezier(45.000,30.000)(45.000,38.284)(39.142,44.142)\qbezier(39.142,44.142)(33.284,50.000)(25.000,50.000)\qbezier(25.000,50.000)(16.716,50.000)(10.858,44.142)\qbezier(10.858,44.142)( 5.000,38.284)( 5.000,30.000)\qbezier( 5.000,30.000)( 5.000,21.716)(10.858,15.858)\qbezier(10.858,15.858)(16.716,10.000)(25.000,10.000)\put(25,30){\line(5, - 4){16}}\put(25,30){\circle*{1}}\put(24,32){\sf\large{O}}\put(15,40){\sf\large{Major Sector}}\put(5,14){\sf\large{A}}\put(25,30){\line(- 5, -4){16}}\put(43,14){\sf\large{B}}\put(14,16){\sf\large{Minor Sector}}\end{picture}
- Tangent to a circle from a point :
\setlength{\unitlength}{1.1mm}\begin{picture}(50,55)\thicklines\qbezier(25.000,10.000)(33.284,10.000)(39.142,15.858)\qbezier(39.142,15.858)(45.000,21.716)(45.000,30.000)\qbezier(45.000,30.000)(45.000,38.284)(39.142,44.142)\qbezier(39.142,44.142)(33.284,50.000)(25.000,50.000)\qbezier(25.000,50.000)(16.716,50.000)(10.858,44.142)\qbezier(10.858,44.142)( 5.000,38.284)( 5.000,30.000)\qbezier( 5.000,30.000)( 5.000,21.716)(10.858,15.858)\qbezier(10.858,15.858)(16.716,10.000)(25.000,10.000)\put(25,30){\line(1,3){6.4}}\put(25,30){\line(1, - 3){6.4}}\put(20,7){\line(3,1){68.5}}\put(20,52.8){\line(3, - 1){68.5}}\put(25,30){\circle*{1}}\put(88,30){\circle*{1.2}}\put(22,30){\sf O}\put(31,6){\sf A}\put(31,52){\sf B}\put(90,28.5){\sf P}\multiput(25,30)(3,0){21}{\line(2,0){1.8}}\qbezier(81.5,32)(78,30)(81,27.5)\qbezier(76,30)(74.5,28)(76,26)\put(33,45){\line(1,3){1.1}}\put(30,45.8){\line(3, - 1){3.2}}\put(30.5,14){\line(3,1){3.2}}\put(33.5,15){\line(1, - 3){1.1}}\put(21,18){\sf 6 cm}\put(73,30.8){\sf 120^\circ$}\put(69,26){\sf 60^\circ$}\end{picture}
- Parallelogram related :
\setlength{\unitlength}{1 cm}\begin{picture}(20,15)\thicklines\qbezier(1,1)(1,1)(6,1)\qbezier(1,1)(1,1)(2,4)\qbezier(2,4)(1.6,4)(7,4)\qbezier(6,1)(6,1)(7,4)\qbezier(2,4)(2,4)(2,1)\qbezier(2,4)(1.6,4)(6.5,2.5)\put(0.7,0.5){\sf B}\put(6,0.5){\sf C}\put(1.8,4.3){\sf A}\put(7,4.3){\sf D}\put(2,0.5){\sf N}\put(3.3,0.5){\sf x cm}\put(6.7,1.5){\sf y cm}\put(6.8,2.4){\sf M}\put(2.2,2.2){\sf z cm}\end{picture}
- Cyclic quadrilateral :
\setlength{\unitlength}{1.5cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\put(-1.58,1.7){\line(1,0){3.15}}\put(-1.9,-1.3){\line(1,0){3.8}}\qbezier(-1.58,1.7)(-1.58,1.7)(-1.9,-1.3)\qbezier(1.57,1.7)(1.57,1.7)(1.9,-1.3)\qbezier(-1.45,-1.3)(-1.4,-0.9)(-1.85,-0.85)\put(-1.4,-0.9){$\bf\large X^{\circ}$}\end{picture}
- Math code :
\setlength{\unitlength}{0.8cm}\begin{picture}(0,0)\thicklines\qbezier(0.2,0)(0.3,2)(2,2)\qbezier(2,2)(3.7,2)(3.8,0)\put(0.2,0){\line(-1,0){3}}\multiput(-2.8,0)(6.6,0){2}{\line(0,-1){3}}\put(-2.8,-3){\line(1,0){6.6}}\put(-2.78,-3){\framebox(0.5,0.5)}\put(0,0.3){\vector(-1,0){2.8}}\put(0,0.3){\vector(1,0){0.1}}\put(-2.8,-3.3){\vector(1,0){6.6}}\put(-2.8,-3.3){\vector(-1,0){0.1}}\put(-3.2,-3){\vector(0,1){3}}\put(-3.2,-3){\vector(0,-2){0.1}}\put(-1.5,0.5){\bf x}\put(0,-4){\bf z}\put(-3.8,-1.6){\bf y}\end{picture}
- Math Code :
\setlength{\unitlength}{1.2cm}\begin{picture}(0,0)\thicklines\qbezier(0,2)(-1.7,1.7)(-1.8,0)\qbezier(-1.8,0)(-1.7,-1.7)(0,-2)\qbezier(0,2)(0,2)(4,0)\qbezier(0,-2)(0,-2)(4,0)\multiput(0,2)(0,-0.29){14}{\line(0,-1){0.18}}\multiput(0,0)(0.31,0){13}{\line(1,0){0.18}}\put(0.2,-0.2){\vector(1,0){3.8}}\put(0.2,-0.2){\vector(-1,0){0.1}}\put(1.6,-0.5){\bf y}\linethickness{0.3mm}\qbezier(4,0.2)(4,0.2)(0.1,2.2)\put(4,0.2){\vector(3,-2){0.1}}\put(0.1,2.2){\vector(-3,2){0.1}}\put(2,1.4){\bf x}\put(-0.5,-0.1){\bf O}\put(4.5,-0.1){\bf P}\end{picture}
- Math Code :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\qbezier(-3,1.5)(0,0)(3,1.5)\qbezier(-3,1.5)(-2.5,4)(0,4.2)\qbezier(3,1.5)(2.5,4)(0,4.2)\put(-3.5,-4.3){\framebox(6,5)}\qbezier(-3.5,0.7)(-3.5,0.7)(-3,1.5)\multiput(2.5,-4.3)(0,5){2}{\line(2,3){1.5}}\put(4,-2.05){\line(0,1){5}}\put(4,2.95){\line(-1,0){1.5}}\multiput(-3,1.5)(0.3,0){20}{\line(1,0){0.2}}\put(-0.5,2){\bf x\ cm}\put(-3.3,0){\vector(1,0){5.7}}\put(-3.3,0){\vector(-1,0){0.1}}\put(-0.9,-0.6){\bf x\ cm}\end{picture}
- Formulas related to SA & Volume :
- Random code :
- Law's of exponents :
\begin{gathered}\boxed{\begin{minipage}{5 cm}\bf{\dag}\:\:\underline{\text{Law of Exponents :}}\\\\\bigstar\:\:\sf\dfrac{a^m}{a^n} = a^{m - n}\\\\\bigstar\:\:\sf{(a^m)^n = a^{mn}}\\\\\bigstar\:\:\sf(a^m)(a^n) = a^{m + n}\\\\\bigstar\:\:\sf\dfrac{1}{a^n} = a^{-n}\\\\\bigstar\:\:\sf\sqrt[\sf n]{\sf a} = (a)^{\dfrac{1}{n}}\end{minipage}}\end{gathered
- Circle with diameter :
\setlength{\unitlength}{1mm}\begin{picture}(50,55)\linethickness{0.4mm}\qbezier(45,30)(45,30)(5,30)\qbezier(25.000,10.000)(33.284,10.000)(39.142,15.858)\qbezier(39.142,15.858)(45.000,21.716)(45.000,30.000)\qbezier(45.000,30.000)(45.000,38.284)(39.142,44.142)\qbezier(39.142,44.142)(33.284,50.000)(25.000,50.000)\qbezier(25.000,50.000)(16.716,50.000)(10.858,44.142)\qbezier(10.858,44.142)( 5.000,38.284)( 5.000,30.000)\qbezier( 5.000,30.000)( 5.000,21.716)(10.858,15.858)\qbezier(10.858,15.858)(16.716,10.000)(25.000,10.000)\multiput(5,30)(20,0){3}{\circle*{1}}\end{picture}
- Fraction rules :
\boxed{\begin{minipage}{6 cm}\bf{\dag}\:\:\underline{\textsf{Fraction Rules :}}\\\\\bigstar\:\:\sf\dfrac{A}{C} + \dfrac{B}{C} = \dfrac{A+B}{C} \\\\\bigstar\:\:\sf{\dfrac{A}{C} - \dfrac{B}{C} = \dfrac{A-B}{C}}\\\\\bigstar\:\:\sf\dfrac{A}{B} \times \dfrac{C}{D} = \dfrac{AC}{BD}\\\\\bigstar\:\:\sf\dfrac{A}{B} + \dfrac{C}{D} = \dfrac{AD}{BD} + \dfrac{BC}{BD} = \dfrac{AD+BC}{BD} \\\\\bigstar\:\:\sf\dfrac{A}{B} - \dfrac{C}{D} = \dfrac{AD}{BD} - \dfrac{BC}{BD} = \dfrac{AD-BC}{BD}\\\\\bigstar \:\:\sf \dfrac{A}{B} \div \dfrac{C}{D} = \dfrac{A}{B} \times \dfrac{D}{C} = \dfrac{AD}{BC}\end{minipage}}
- Frustum :
\setlength{\unitlength}{1cm}\begin{picture}\linethickness{0.4mm}\qbezier( - 1, 0)( - 1,0)(1,3)\qbezier(5.2, 0)(5.2,0)(3,3)\qbezier(1, 3)(2,2.5)(3,3)\qbezier(1, 3)(2,3.5)(3,3)\qbezier( - 1, 0)(1.8, 0.8)(5.2,0)\qbezier( - 1, 0)(1.8, - 1)(5.2,0)\qbezier(4.8, 0)( - 1, 0)(5.2,0)\qbezier(3, 3)(1, 3)(3,3)\put(2,0){\dashbox{0.2}(1,3)}\put(2,0){\circle*{0.19}}\put(2,2.99){\circle*{0.19}}\put(1.2,1.3){\bf H}\put(3.2,-1){\bf R}\put(2.3,3.4){\bf\large r}\end{picture}
- Rhombus with diagonal :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\put(0,0){\line(1,3){1.5}}\put(0,0){\line(1,0){5}}\put(5,0){\line(1,3){1.5}}\put(1.5,4.5){\line(1,0){5}}\qbezier(1.56,4.5)(1.56,4.5)(5,0)\qbezier(6.45,4.5)(6.45,4.5)(0,0)\put(-0.5,-0.5){\sf B}\put(1,4.8){\sf A}\put(5.2,-0.5){\sf C}\put(6.7,4.75){\sf D}\put(3,1.6){\sf O}\end{picture}
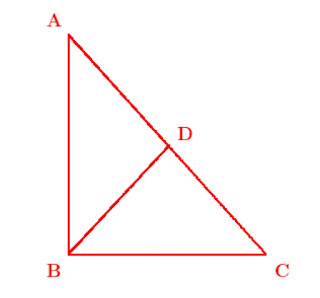
- Triangle related :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\put(0,0){\line(1,0){4.5}}\put(0,0){\line(0,1){5}}\qbezier(0,5)(0,5)(4.5,0)\qbezier(0,0)(0,0)(2.3,2.48)\put(-0.5,5.2){\bf A}\put(-0.5,-0.5){\bf B}\put(4.7,-0.5){\bf C}\put(2.5,2.6){\bf D}\end{picture}
- Triangle related :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\put(0,0){\line(1,0){5}}\put(1.2,2.5){\line(1,0){2.6}}\qbezier(0,0)(0,0)(2.5,5)\qbezier(2.5,5)(2.5,5)(5,0)\qbezier(1.2,2.5)(1.2,2.5)(5,0)\qbezier(0,0)(0,0)(3.8,2.5)\put(2.3,5.3){\bf A}\put(-0.5,-0.5){\bf B}\put(5.3,-0.5){\bf C}\put(0.5,2.5){\bf D}\put(4.2,2.5){\bf E}\end{picture}
- Rhombus :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\put(0,0){\line(1,3){1.5}}\put(0,0){\line(1,0){5}}\put(5,0){\line(1,3){1.5}}\put(1.5,4.5){\line(1,0){5}}\put(-0.5,-0.5){\sf D}\put(1,4.8){\sf A}\put(5.2,-0.5){\sf C}\put(6.7,4.75){\sf B}\end{picture}
- Pentagon :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\put(0,0){\line(1,0){4}}\qbezier(0,0)(0,0)(-1,3)\qbezier(4,0)(4,0)(5,3)\qbezier(-1,3)(-1,3)(2,5)\qbezier(5,3)(5,3)(2,5)\put(1.8,5.3){\bf A}\put(5.25,2.9){\bf B}\put(-1.55,2.9){\bf E}\put(-0.5,-0.5){\bf D}\put(4.3,-0.5){\bf C}\end{picture}
- Rectangular Prism :
\setlength{\unitlength}{1cm}\begin{picture}\thicklines\multiput(0,0)(2.6,0){2}{\line(0,1){5}}\multiput(0,0)(0,5){2}{\line(1,0){2.6}}\multiput(1.4,1.4)(0,5){2}{\line(1,0){2.6}}\multiput(1.4,1.4)(2.6,0){2}{\line(0,1){5}}\multiput(0,0)(0,5){2}{\line(1,1){1.4}}\multiput(2.6,0)(0,5){2}{\line(1,1){1.4}}\put(-0.5,-0.4){\sf A}\put(1.4,0.85){\sf D}\put(2.8,-0.4){\sf B}\put(4.1,1){\sf C}\put(1.4,6.55){\sf H}\put(4.1,6.5){\sf G}\put(-0.4,5.1){\sf E}\put(2.85,4.7){\sf F}\put(1,-0.5){\sf Length}\put(3.5,0.35){\sf Breadth}\put(4.3,3.5){\sf Height}\end{picture}
- Formulas of Statistics :
\boxed {\begin{minipage}{9.2 cm}\\ \dag \: \underline{\Large\bf Formulas\:of\:Statistics} \\ \\ \bigstar \: \underline{\rm Mean:} \\ \\ \bullet\sf M=\dfrac {\Sigma x}{n} \\ \bullet\sf M=a+\dfrac {\Sigma fy}{\Sigma f} \\ \\ \bullet\sf M=A +\dfrac {\Sigma fy^i}{\Sigma f}\times c \\ \\ \bigstar \: \underline{\rm Median :} \\ \\ \bullet\sf M_d=\dfrac {n+1}{2} \:\left[\because n\:is\:odd\:number\right] \\ \bullet\sf M_d=\dfrac {1}{2}\left (\dfrac {n}{2}+\dfrac {n}{2}+1\right)\:\left[\because n\:is\:even\:number\right] \\ \\ \bullet\sf M_d=l+\dfrac {m-c}{f}\times i \\ \\ \bigstar \: {\boxed{\sf M_0=3M_d-2M}}\end {minipage}}
- Hexagon :
\setlength{\unitlength}{6mm}\begin{picture}\thicklines\qbezier(-4,0)(-3,1.8)(-2,3.5)\qbezier(-4,0)(-3,-1.8)(-2,-3.5)\qbezier(-2,-3.5)(0,-3.5)(2,-3.5)\qbezier(2,-3.5)(3,-1.8)(4,0)\qbezier(4,0)(3,1.8)(2,3.5)\qbezier(-2,3.5)(0,3.5)(2,3.5)\put(-2.8,3.7){\bf A}\put(2.4,3.7){\bf B}\put(2.3,-4.2){\bf D}\put(-2.7,-4.2){\bf E}\put(4.4,-0.1){\bf C}\put(-4.75,-0.1){\bf F}\end{picture}
- Octagon :
\setlength{\unitlength}{10mm}\begin{picture}(0,0)\thicklines\qbezier(-3,-1.3)(-3,0)(-3,1.3)\qbezier(-3,1.3)(-2,2.3)(-1.3,3)\qbezier(-1.3,3)(0,3)(1.3,3)\qbezier(1.3,3)(2,2.3)(3,1.3)\qbezier(3,1.3)(3,0)(3,-1.3)\qbezier(3,-1.3)(2,-2.3)(1.3,-3)\qbezier(1.3,-3)(0,-3)(-1.3,-3)\qbezier(-1.3,-3)(-2,-2.3)(-3,-1.3)\put(1.5,3.25){\bf B}\put(-1.8,3.25){\bf A}\put(1.5,-3.5){\bf E}\put(-1.8,-3.4){\bf F}\put(3.3,1.3){\bf C}\put(3.3,-1.6){\bf D}\put(-3.65,1.35){\bf H}\put(-3.65,-1.45){\bf G}\end{picture}
- Circle related :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\qbezier(1.6,-1.6)(1.6,-1.6)(1.6,1.6)\qbezier (-1.6,-1.6)(-1.6,-1.6)(-1.6,1.6)\qbezier (-1.6,-1.6)(-1.6,-1.6)(1.6,-1.6)\qbezier (-1.6,1.6)(-1.6,1.6)(1.6,1.6)\put (-2.1,1.8){\sf A}\put (1.8,1.75){\sf B}\put (1.9,-2){\sf C}\put (-2.1,-2.05){\sf D}\qbezier (-1.6,1.6)(-1.6,1.6)(1.6,-1.6)\put (0,0){\circle*{0.15}}\put (0.15,0.1){\bf O}\end{picture}
- Trapezium related :
\setlength{\unitlength}{1.1 cm}\begin{picture}(0,0)\linethickness{0.4mm}\qbezier(0,0)(0,0)(1.5,3)\qbezier(7,0)(7,0)(5.5,3)\qbezier(1.5,3)(1.5,3)(5.5,3)\qbezier(7,0)(7,0)(0,0)\put(1.3,3.2){$\sf A$}\put(-0.35,-0.35){$\sf B$}\put(1.5,-0.4){$\sf C$}\put(5.3,-0.4){$\sf D$}\put(5.45,3.15){$\sf F$}\put(7.2,-0.34){$\sf E$}\qbezier(5.5,0)(5.5,0)(5.5,3)\qbezier(1.5,0)(1.5,0)(1.5,3)\put(3.2, 3.2){$\sf x \: cm$}\put(2, - 0.3){\vector(1,0){3}}\put(2, - 0.3){\vector(-1,0){0}}\put(3.2,-0.7){$\sf x \: cm$}\put(5.7,-0.3){\vector(1,0){1.2}}\put(5.7,-0.3){\vector(-1,0){0}}\put(6,-0.7){$\sf y \: cm$}\put(0.2, - 0.3){\vector(1,0){1.2}}\put(0.2,-0.3){\vector(-1,0){0}}\put(0.55,-0.7){$\sf y \: cm$}\put(0.2, - 1){\vector(1,0){6.7}}\put(0.2, - 1){\vector(-1,0){0}}\put(3,-1.45){$\sf x+2y \: cm$}\put(1.7, 1.4){$\sf z \: cm$}\put(4.55,1.4){\sf z\:cm}\end{picture}
- Parallel lines and triangles :
\setlength{\unitlength}{20mm}\begin{picture}\thicklines \put(0,0){\line(1,0){2.5}}\put(0,2.5){\line(1,0){2.5}} \put(0,0){\line(1,2){1.25}}\put(2.5,0){\line(-1,2){1.25}}\put(1.25,0){\line(0,1){2.5}}\put(-0.25,-0.25){\bf{B}}\put(1.18,2.6){\bf{A}}\put(2.55,-0.25){\bf{C}}\put(1.18,-0.25){\bf{D}}\qbezier(0.9,2.5)(0.8,2.3)(1.07,2.15)\qbezier(1.6,2.5)(1.67,2.2)(1.45,2.15)\put(0.6,2.1){$\bf x^{\circ}$}\put(1.7,2.1){$\bf y^{\circ}$}\qbezier(0.17,0.3)(0.37,0.3)(0.4,0)\qbezier(2.06,0)(2.2,0.3)(2.35,0.3)\put(0.5,0.3){$\bf x^{\circ}$}\put(1.87,0.27){$\bf y^{\circ}$}\end{picture}
- Integrals :
\boxed{\boxed{\begin{minipage}{4cm}\displaystyle\circ\sf\:\int{1\:dx}=x+c\\\\\circ\sf\:\int{a\:dx}=ax+c\\\\\circ\sf\:\int{x^n\:dx}=\dfrac{x^{n+1}}{n+1}+c\\\\\circ\sf\:\int{sin\:x\:dx}=-cos\:x+c\\\\\circ\sf\:\int{cos\:x\:dx}=sin\:x+c\\\\\circ\sf\:\int{sec^2x\:dx}=tan\:x+c\\\\\circ\sf\:\int{e^x\:dx}=e^x+c\end{minipage}}}
- Rectangle related :
\setlength{\unitlength}{1.2cm}\begin{picture}(0,0)\thicklines\put(0.6,0.9){\sf C}\put(4.17,0.9){\sf D}\put(4.17,3){\sf B}\put(0.6,3){\sf A}\qbezier(1,1)(1,1)(4,1)\qbezier(4,1)(4,1)(4,3)\qbezier(4,3)(4,3)(1,3)\qbezier(1,3)(1,3)(1,1)\qbezier(1,3)(1,3)(4,1)\put(5,2){\sf\large =}\qbezier(6,1)(6,1)(6,3)\qbezier(6,3)(6,3)(9,1)\qbezier(9,1)(9,1)(6,1)\put(5.8,3.1){\sf A}\put(5.55,0.85){\sf C}\put(9.2,0.8){\sf D}\put(9,2){\sf\large +}\qbezier(10,3)(10,3)(13,3)\qbezier(13,3)(13,3)(13,1)\qbezier(13,1)(13,1)(10,3)\put(12.8,0.5){\sf D}\put(13.1,3.1){\sf B}\put(9.8,3.1){\sf A}\end{picture}
- Sphere :
\setlength{\unitlength}{1.2cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\qbezier(-2.3,0)(0,-1)(2.3,0)\qbezier(-2.3,0)(0,1)(2.3,0)\thinlines\qbezier (0,0)(0,0)(0.2,0.3)\qbezier (0.3,0.4)(0.3,0.4)(0.5,0.7)\qbezier (0.6,0.8)(0.6,0.8)(0.8,1.1)\qbezier (0.9,1.2)(0.9,1.2)(1.1,1.5)\qbezier (1.2,1.6)(1.2,1.6)(1.38,1.9)\put(0.2,1){\bf R}\end{picture}
- Natural logarithm :
\boxed{\boxed{\begin{minipage}{4.2cm}\circ\sf\:\ln 1=0\\\circ\sf\:\ln e=1\\\circ\sf\:\ln x=y\leftrightarrow e^y=x\\\circ\sf\:e^{\ln x}=x,\:x>0\\\circ\sf\:\ln(e^x)=x,\:x\in\mathbb{\large R}\\\circ\sf\:\ln(xy)=\ln x+\ln y\\\circ\sf\:\ln(x/y)=\ln x-\ln y\\\circ\sf\:\ln(x^r)=r\ln x\\\circ\sf\:\ln x=log_e\:x\end{minipage}}}
- Obtuse angle :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\linethickness{.4mm}\qbezier(1,1)(1,1)(5.5,1)\qbezier(1,1)(1,1)( -1,4)\qbezier(0.65,1.55)(1.5,1.8)(2,1)\put(3,3){\bf Obtuse Angle :}\put(3,2.5){\sf measures more than}\put(3,2){\sf 90 degrees}\end{picture}
- Profit and loss :
\boxed{\begin{minipage}{5cm}\bigstar$\:\underline{\textbf{Profit and Loss Formulas :}}\\\\ \\ \sf {\textcircled{\footnotesize\textsf{1}}} \:S.P. =$\sf \bigg\lgroup\dfrac{100 + Profit \%}{100}\bigg\rgroup \times 100$\\\\\\ \sf {\textcircled{\footnotesize\textsf{2}}} \:\:C.P. = $\sf \dfrac{S.P. \times 100}{100 + Profit \%}$\\\\\\\sf{\textcircled{\footnotesize\textsf{3}}} \:\:Profit = $\sf \dfrac{Profit \% \times C.P.}{100}$\\\\\\ \sf{\textcircled{\footnotesize\textsf{4}}} \: \:Profit (gain) = S.P. - C.P. \\\\\\\sf{\textcircled{\footnotesize\textsf{5}}} \: \:$\sf Profit \% = \dfrac{Profit}{C.P.} \times 100$\end{minipage}}
- Formulas (Cylinder) :
\boxed{\begin{minipage}{6.2 cm}\bigstar$\:\underline{\textbf{Formulae Related to Cylinder :}}\\\\\sf {\textcircled{\footnotesize\textsf{1}}} \:Area\:of\:Base\:and\:top =\pi r^2 \\\\ \sf {\textcircled{\footnotesize\textsf{2}}} \:\:Curved \: Surface \: Area =2 \pi rh\\\\\sf{\textcircled{\footnotesize\textsf{3}}} \:\:Total \: Surface \: Area = 2 \pi r(h + r)\\ \\{\textcircled{\footnotesize\textsf{4}}} \: \:Volume=\pi r^2h\end{minipage}}
- Median :
\boxed{\begin{minipage}{6cm}$\bigstar$\:\:\sf Median = l + $\sf\dfrac{\frac{n}{2}-C.f.}{f}\times h\\\\Here: \\1)\:n = \sum f =\\2)\:l=Lower\:limit\:of\:median\:class=\\3)\:C.f.=Cumulative\:frequency\:of\:class\\preceeding\:the\:median\:class=\\4)\:f= frequency\:of\:median\:class=\\5)\:h= Class\:interval = \end{minipage}}
- Right angle :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\linethickness{.4mm}\put(1,1){\line(1,0){4.5}}\put(1,1){\line(0,1){3.5}}\put(1.02,1.02){\framebox(0.3,0.3)}\put(3,3.5){\bf Right Angle :}\put(3,3){\sf measures exactly}\put(3,2.5){\sf 90 degrees}\end{picture}
- The CAST diagram :
\setlength{\unitlength}{7mm}\begin{picture}(0,0)\thicklines\put(0,0){\vector(1,0){6}}\put(0,0){\vector(-1,0){6}}\put(0,0){\vector(0,1){6}}\put(0,0){\vector(0,-1){6}}\put( -3,4){\sf\huge S}\put(3,4){\sf\huge A}\put( -3, - 2){\sf\huge T}\put(3, - 2){\sf\huge C}\put( -4.5,2.5){\sf\large Sin is positive}\put(1.5,2.5){\sf\large All are positive}\put( -4.5, - 3){\sf\large Tan is positive}\put(2, - 3){\sf\large Cos is positive}\put( -4.1,1.5){\sf Cos and Tan }\put( -4.1,1){\sf are negative}\put( -4.1, -4){\sf Sin and Cos}\put( -4.1, - 4.5){\sf are negative}\put(2.4, - 4){\sf Sin and Tan}\put(2.4, - 4.5){\sf are negative}\end{picture}
- Diff. Formulas (Trigonometry) :
\boxed{\boxed{\begin{minipage}{5cm}\displaystyle\circ\sf\;\dfrac{d}{dx}(sin\;x)=cosx \\\\ \circ \;\dfrac{d}{dx}(cos\;x) = -sinx \\\\ \circ \; \dfrac{d}{dx}(tan\;x) = sec^{2}x \\\\ \circ\; \dfrac{d}{dx}(cot\;x) = -csc^{2}x \\\\ \circ \; \dfrac{d}{dx}(sec\;x) = secx \cdot tanx \\\\ \circ \; \dfrac{d}{dx}(csc\;x) = -cscx \cdot cotx \\\\ \circ\; \dfrac{d}{dx}(sinh\;x)=coshx \\\\ \circ\; \dfrac{d}{dx}(cosh\;x)= sinhx \\\\ \circ\;\dfrac{d}{dx}(tanh\;x)=sech^{2}h \\\\ \circ\;\dfrac{d}{dx}(coth\;x)=-csch^{2}x \\\\ \circ\;\dfrac{d}{dx}(sech\;x) =-sechx \cdot tanhx \\\\ \circ\;\dfrac{d}{dx}(csch\;x) = -cschx \cdot cothx\end{minipage}}}
- Interior angles (C) :
\setlength{\unitlength}{8mm}\begin{picture}(0,0)\thicklines\put(2,4){\line(7,0){5}}\put(0,0){\line(6,0){6}}\qbezier(2,4)(2,4)(0,0)\qbezier(0.9,0)(1.1,0.6)(0.4,0.8)\qbezier(1.69,3.2)(2.5,3.2)(2.75,4)\put(3,0){\vector(3,0){1}}\put(5,4){\vector(3,0){1}}\end{picture}
- Alternate angles (Z) :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\multiput(0,0)(0,3){2}{\line(1,0){4}}\qbezier(0,0)(0,0)(4,3)\qbezier(1,0)(1.2,0.35)(0.8,0.6)\qbezier(3,3)(2.8,2.65)(3.2,2.4)\put(2.5,0.02){\vector(1,0){0}}\put(1.5,3.02){\vector(-1,0){0}}\end{picture}
- Logarithm equations :
\boxed{\boxed{\begin{minipage}{5cm}\displaystyle\circ\sf\ ^{a} log \ a= 1\\\\\circ \ ^{a}log \ 1 = 0 \\\\\circ \ ^{a ^{n}} log \ b^{m}= \dfrac{m}{n} \times\:^{a}log \ b \\\\\circ \ ^{a^{m}} \ log \ b^{m} = \ ^{a}log \ b \\\\\circ \ ^{a}log \ b = \dfrac{1}{^{b}log \ a} \\\\\circ \ ^{a}log \ b = \dfrac{^{m}log \ b}{^{m} log \ a} \\\\\circ \ a^{^{a} logb} = b \\\\\circ \ ^{a}log \ b + ^{a}log \ c = \ ^{a}log(bc) \\\\\circ \ ^{a}log \ b -\: ^{a}log \ c = \ ^{a}log \left( \dfrac{b}{c} \right) \\\circ \ ^{a}log \ b \:\cdot\: ^{a}log \ c = \ ^{a}log \ c \\\\\circ \ ^{a}log \left( \dfrac{b}{c} \right) = \ ^{a}log \left(\dfrac{c}{b}\right)\end{minipage}}}
- Linear Pair :
\setlength{\unitlength}{1 cm}\begin{picture}(0,0)\thicklines\put(5,1){\vector(1,0){4}}\put(5,1){\vector(-1,0){4}}\put(5,1){\vector(1,1){3}}\put(2,2){$\underline{\boxed{\large\sf a + b = 180^{\circ}}$}}\put(4.5,1.3){$\sf a^{\circ}$}\put(5.7,1.3){$\sf b^{\circ}$}\end{picture}
- Corresponding angles (F) :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\qbezier(0,0)(0,0)(2,5)\put(2,5){\line(1,0){4}}\put(1,2.5){\line(1,0){4}}\qbezier(1.8,2.5)(1.8,1.85)(0.75,1.88)\qbezier(2.8,5)(2.8,4.3)(1.75,4.3)\put(4,5){\vector(1,0){0}}\put(3.5,2.52){\vector(1,0){0}}\end{picture}
- Acute angle :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\linethickness{.4mm}\qbezier(1,1)(1,1)(5.5,1)\qbezier(1,1)(1,1)(5,4)\qbezier(1.7,1.55)(2.2,1.3)(2,1)\put(5,3){\bf Acute Angle :}\put(4.9,2.5){\sf measures less than}\put(5,2){\sf 90 degrees}\end{picture}
- Formulas (Cone) :
\boxed{\begin{minipage}{6 cm}\bigstar$\:\underline{\textbf{Formulae Related to Cone :}}\\\\\sf {\textcircled{\footnotesize\textsf{1}}} \:Area\:of\:Base =\pi r^2 \\\\ \sf {\textcircled{\footnotesize\textsf{2}}} \:\:Curved \: Surface \: Area = \pi rl\\\\\sf{\textcircled{\footnotesize\textsf{3}}} \:\:TSA = Area\:of\:Base + CSA=\pi r^2+\pi rl\\ \\{\textcircled{\footnotesize\textsf{4}}} \: \:Volume=\dfrac{1}{3}\pi r^2h\\ \\{\textcircled{\footnotesize\textsf{5}}} \: \:Slant \: Height=\sqrt{r^2 + h^2}\end{minipage}}
- Anchor chart on real numbers :
\setlength{\unitlength}{15mm}\begin{picture}(10,10)\thicklines \put(0,8){\framebox{\framebox{\large{\bf{Natural}}}}}\put(0.6,7.3){\huge{$\downarrow$}} \put(0.1,6.6){\framebox{\framebox{\large{\bf{Whole}}}}}\put(0.6,5.9){\huge{$\downarrow$}} \put(0.05,5.15){\framebox{\framebox{\large{\bf{Integer}}}}} \put(0.6,4.3){\huge{$\downarrow$}}\put(-0.05,3.5){\framebox{\framebox{\large{\bf{Rational}}}}}\put(2.8,3.5){\framebox{\framebox{\large{\bf{Irrational}}}}}\put(0.6,2.7){\huge{$\downarrow$}}\put(3.5,2.7){\huge{$\downarrow$}}\put(-0.3,1.8){\framebox{\framebox{\huge{\bf{\quad Real\:numbers\quad}}}}}\end{picture}
- Distance and height :
\setlength{\unitlength}{15mm}\begin{picture}(8,8)\thicklines\put(0,0){\line(1,0){4}}\put(4,0){\line(0,1){1.65}}\put(4,2.13){\line(0,1){1.44 }}\qbezier(0,0)(2,1.9)(3.77,3.8)\qbezier(0,0)(1,0.45)(3.77,1.9) \put(3.7,0){\line(0,1){0.3}}\put(3.7,0.3){\line(1,0){0.3}}\qbezier(0.6,0)(0.6,0.4)(0.4,0.4)\qbezier(0.8,0)(0.8,0.2)(0.7,0.33)\put(0.9,0.2){$30^{\circ}$}\put(0.8,0.6){$60^{\circ}$} \put(2,-0.3){\bf{x}}\put(4,1.9){\circle{0.5}} \put(4,3.8){\circle{0.5}}\put(4.2,1){$\bf{h_1}$} \put(4.2,2.8){$\bf{h_2}$}\end{picture}
- Formulas of area :
\boxed{\begin {minipage}{9cm}\\ \dag\quad \Large\underline{\bf Formulas\:of\:Areas:-}\\ \\ \star\sf Square=(side)^2\\ \\ \star\sf Rectangle=Length\times Breadth \\\\ \star\sf Triangle=\dfrac{1}{2}\times Breadth\times Height \\\\ \star \sf Scalene\triangle=\sqrt {s (s-a)(s-b)(s-c)}\\ \\ \star \sf Rhombus =\dfrac {1}{2}\times d_1\times d_2 \\\\ \star\sf Rhombus =\:\dfrac {1}{2}p\sqrt {4a^2-p^2}\\ \\ \star\sf Parallelogram =Breadth\times Height\\\\ \star\sf Trapezium =\dfrac {1}{2}(a+b)\times Height \\ \\ \star\sf Equilateral\:Triangle=\dfrac {\sqrt{3}}{4}(side)^2\end {minipage}}
- Rectangle with diagonals :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\qbezier (0,0)(0,0)(5,0)\qbezier (0,0)(0,0)(0,3)\qbezier (0,3)(0,3)(5,3)\qbezier (5,3)(5,3)(5,0)\qbezier (0,3)(5,0)(5,0)\qbezier (0,0)(0,0)(5,3)\put (-0.4,-0.2){\sf D}\put (-0.2,3.1){\sf A}\put (5.2,3.1){\sf B}\put (5.2,-0.2){\sf C}\put (2.4,1){\sf O}\put (2,-0.4){\bf x\:cm}\put (-1,1.5){\sf y\:cm}\end {picture}
- Cylinder inside hollow cylinder :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\multiput(0,0)(4,0){2}{\line(0,1){6}}\multiput(1,0)(2,0){2}{\line(0,1){6}}\multiput(0,0)(0,6){2}{\qbezier(0,0)(2,-0.6)(4,0)}\multiput(0,0)(0,6){2}{\qbezier(0,0)(2,0.6)(4,0)}\multiput(1,0)(0,6){2}{\qbezier(0,0)(1,-0.2)(2,0)}\multiput(1,0)(0,6){2}{\qbezier(0,0)(1,0.2)(2,0)}\multiput(2,0.07)(0,0.3){20}{\line(0,1){0.2}}\multiput(2,4)(0.3,0){7}{\line(1,0){0.2}}\multiput(2,2)(-0.27,0){4}{\line(-1,0){0.2}}\put(1.4,1.5){\bf\large r}\put(3.35,3.45){\bf R}\put(1.4,3){\bf H}\end{picture}
- Fraction rules :
\boxed{\begin{minipage}{6 cm}\bf{\dag}\:\:\underline{\textsf{Fraction Rules :}}\\\\\bigstar\:\:\sf\dfrac{A}{C} + \dfrac{B}{C} = \dfrac{A+B}{C} \\\\\bigstar\:\:\sf{\dfrac{A}{C} - \dfrac{B}{C} = \dfrac{A-B}{C}}\\\\\bigstar\:\:\sf\dfrac{A}{B} \times \dfrac{C}{D} = \dfrac{AC}{BD}\\\\\bigstar\:\:\sf\dfrac{A}{B} + \dfrac{C}{D} = \dfrac{AD}{BD} + \dfrac{BC}{BD} = \dfrac{AD+BC}{BD} \\\\\bigstar\:\:\sf\dfrac{A}{B} - \dfrac{C}{D} = \dfrac{AD}{BD} - \dfrac{BC}{BD} = \dfrac{AD-BC}{BD}\\\\\bigstar \:\:\sf \dfrac{A}{B} \div \dfrac{C}{D} = \dfrac{A}{B} \times \dfrac{D}{C} = \dfrac{AD}{BC}\end{minipage}}
- Frustum :
\setlength{\unitlength}{1cm}\begin{picture}\linethickness{0.4mm}\qbezier( - 1, 0)( - 1,0)(1,3)\qbezier(5.2, 0)(5.2,0)(3,3)\qbezier(1, 3)(2,2.5)(3,3)\qbezier(1, 3)(2,3.5)(3,3)\qbezier( - 1, 0)(1.8, 0.8)(5.2,0)\qbezier( - 1, 0)(1.8, - 1)(5.2,0)\qbezier(4.8, 0)( - 1, 0)(5.2,0)\qbezier(3, 3)(1, 3)(3,3)\put(2,0){\dashbox{0.2}(1,3)}\put(2,0){\circle*{0.19}}\put(2,2.99){\circle*{0.19}}\put(1.2,1.3){\bf H}\put(3.2,-1){\bf R}\put(2.3,3.4){\bf\large r}\end{picture}
- Rhombus with diagonal :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\put(0,0){\line(1,3){1.5}}\put(0,0){\line(1,0){5}}\put(5,0){\line(1,3){1.5}}\put(1.5,4.5){\line(1,0){5}}\qbezier(1.56,4.5)(1.56,4.5)(5,0)\qbezier(6.45,4.5)(6.45,4.5)(0,0)\put(-0.5,-0.5){\sf B}\put(1,4.8){\sf A}\put(5.2,-0.5){\sf C}\put(6.7,4.75){\sf D}\put(3,1.6){\sf O}\end{picture}
- Triangle related :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\put(0,0){\line(1,0){4.5}}\put(0,0){\line(0,1){5}}\qbezier(0,5)(0,5)(4.5,0)\qbezier(0,0)(0,0)(2.3,2.48)\put(-0.5,5.2){\bf A}\put(-0.5,-0.5){\bf B}\put(4.7,-0.5){\bf C}\put(2.5,2.6){\bf D}\end{picture}
- Triangle related :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\put(0,0){\line(1,0){5}}\put(1.2,2.5){\line(1,0){2.6}}\qbezier(0,0)(0,0)(2.5,5)\qbezier(2.5,5)(2.5,5)(5,0)\qbezier(1.2,2.5)(1.2,2.5)(5,0)\qbezier(0,0)(0,0)(3.8,2.5)\put(2.3,5.3){\bf A}\put(-0.5,-0.5){\bf B}\put(5.3,-0.5){\bf C}\put(0.5,2.5){\bf D}\put(4.2,2.5){\bf E}\end{picture}
- Rhombus :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\put(0,0){\line(1,3){1.5}}\put(0,0){\line(1,0){5}}\put(5,0){\line(1,3){1.5}}\put(1.5,4.5){\line(1,0){5}}\put(-0.5,-0.5){\sf D}\put(1,4.8){\sf A}\put(5.2,-0.5){\sf C}\put(6.7,4.75){\sf B}\end{picture}
- Pentagon :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\put(0,0){\line(1,0){4}}\qbezier(0,0)(0,0)(-1,3)\qbezier(4,0)(4,0)(5,3)\qbezier(-1,3)(-1,3)(2,5)\qbezier(5,3)(5,3)(2,5)\put(1.8,5.3){\bf A}\put(5.25,2.9){\bf B}\put(-1.55,2.9){\bf E}\put(-0.5,-0.5){\bf D}\put(4.3,-0.5){\bf C}\end{picture}
- Rectangular Prism :
\setlength{\unitlength}{1cm}\begin{picture}\thicklines\multiput(0,0)(2.6,0){2}{\line(0,1){5}}\multiput(0,0)(0,5){2}{\line(1,0){2.6}}\multiput(1.4,1.4)(0,5){2}{\line(1,0){2.6}}\multiput(1.4,1.4)(2.6,0){2}{\line(0,1){5}}\multiput(0,0)(0,5){2}{\line(1,1){1.4}}\multiput(2.6,0)(0,5){2}{\line(1,1){1.4}}\put(-0.5,-0.4){\sf A}\put(1.4,0.85){\sf D}\put(2.8,-0.4){\sf B}\put(4.1,1){\sf C}\put(1.4,6.55){\sf H}\put(4.1,6.5){\sf G}\put(-0.4,5.1){\sf E}\put(2.85,4.7){\sf F}\put(1,-0.5){\sf Length}\put(3.5,0.35){\sf Breadth}\put(4.3,3.5){\sf Height}\end{picture}
- Formulas of Statistics :
\boxed {\begin{minipage}{9.2 cm}\\ \dag \: \underline{\Large\bf Formulas\:of\:Statistics} \\ \\ \bigstar \: \underline{\rm Mean:} \\ \\ \bullet\sf M=\dfrac {\Sigma x}{n} \\ \bullet\sf M=a+\dfrac {\Sigma fy}{\Sigma f} \\ \\ \bullet\sf M=A +\dfrac {\Sigma fy^i}{\Sigma f}\times c \\ \\ \bigstar \: \underline{\rm Median :} \\ \\ \bullet\sf M_d=\dfrac {n+1}{2} \:\left[\because n\:is\:odd\:number\right] \\ \bullet\sf M_d=\dfrac {1}{2}\left (\dfrac {n}{2}+\dfrac {n}{2}+1\right)\:\left[\because n\:is\:even\:number\right] \\ \\ \bullet\sf M_d=l+\dfrac {m-c}{f}\times i \\ \\ \bigstar \: {\boxed{\sf M_0=3M_d-2M}}\end {minipage}}
- Hexagon :
\setlength{\unitlength}{6mm}\begin{picture}\thicklines\qbezier(-4,0)(-3,1.8)(-2,3.5)\qbezier(-4,0)(-3,-1.8)(-2,-3.5)\qbezier(-2,-3.5)(0,-3.5)(2,-3.5)\qbezier(2,-3.5)(3,-1.8)(4,0)\qbezier(4,0)(3,1.8)(2,3.5)\qbezier(-2,3.5)(0,3.5)(2,3.5)\put(-2.8,3.7){\bf A}\put(2.4,3.7){\bf B}\put(2.3,-4.2){\bf D}\put(-2.7,-4.2){\bf E}\put(4.4,-0.1){\bf C}\put(-4.75,-0.1){\bf F}\end{picture}
- Octagon :
\setlength{\unitlength}{10mm}\begin{picture}(0,0)\thicklines\qbezier(-3,-1.3)(-3,0)(-3,1.3)\qbezier(-3,1.3)(-2,2.3)(-1.3,3)\qbezier(-1.3,3)(0,3)(1.3,3)\qbezier(1.3,3)(2,2.3)(3,1.3)\qbezier(3,1.3)(3,0)(3,-1.3)\qbezier(3,-1.3)(2,-2.3)(1.3,-3)\qbezier(1.3,-3)(0,-3)(-1.3,-3)\qbezier(-1.3,-3)(-2,-2.3)(-3,-1.3)\put(1.5,3.25){\bf B}\put(-1.8,3.25){\bf A}\put(1.5,-3.5){\bf E}\put(-1.8,-3.4){\bf F}\put(3.3,1.3){\bf C}\put(3.3,-1.6){\bf D}\put(-3.65,1.35){\bf H}\put(-3.65,-1.45){\bf G}\end{picture}
- Circle related :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\qbezier(1.6,-1.6)(1.6,-1.6)(1.6,1.6)\qbezier (-1.6,-1.6)(-1.6,-1.6)(-1.6,1.6)\qbezier (-1.6,-1.6)(-1.6,-1.6)(1.6,-1.6)\qbezier (-1.6,1.6)(-1.6,1.6)(1.6,1.6)\put (-2.1,1.8){\sf A}\put (1.8,1.75){\sf B}\put (1.9,-2){\sf C}\put (-2.1,-2.05){\sf D}\qbezier (-1.6,1.6)(-1.6,1.6)(1.6,-1.6)\put (0,0){\circle*{0.15}}\put (0.15,0.1){\bf O}\end{picture}
- Trapezium related :
\setlength{\unitlength}{1.1 cm}\begin{picture}(0,0)\linethickness{0.4mm}\qbezier(0,0)(0,0)(1.5,3)\qbezier(7,0)(7,0)(5.5,3)\qbezier(1.5,3)(1.5,3)(5.5,3)\qbezier(7,0)(7,0)(0,0)\put(1.3,3.2){$\sf A$}\put(-0.35,-0.35){$\sf B$}\put(1.5,-0.4){$\sf C$}\put(5.3,-0.4){$\sf D$}\put(5.45,3.15){$\sf F$}\put(7.2,-0.34){$\sf E$}\qbezier(5.5,0)(5.5,0)(5.5,3)\qbezier(1.5,0)(1.5,0)(1.5,3)\put(3.2, 3.2){$\sf x \: cm$}\put(2, - 0.3){\vector(1,0){3}}\put(2, - 0.3){\vector(-1,0){0}}\put(3.2,-0.7){$\sf x \: cm$}\put(5.7,-0.3){\vector(1,0){1.2}}\put(5.7,-0.3){\vector(-1,0){0}}\put(6,-0.7){$\sf y \: cm$}\put(0.2, - 0.3){\vector(1,0){1.2}}\put(0.2,-0.3){\vector(-1,0){0}}\put(0.55,-0.7){$\sf y \: cm$}\put(0.2, - 1){\vector(1,0){6.7}}\put(0.2, - 1){\vector(-1,0){0}}\put(3,-1.45){$\sf x+2y \: cm$}\put(1.7, 1.4){$\sf z \: cm$}\put(4.55,1.4){\sf z\:cm}\end{picture}
- Parallel lines and triangles :
\setlength{\unitlength}{20mm}\begin{picture}\thicklines \put(0,0){\line(1,0){2.5}}\put(0,2.5){\line(1,0){2.5}} \put(0,0){\line(1,2){1.25}}\put(2.5,0){\line(-1,2){1.25}}\put(1.25,0){\line(0,1){2.5}}\put(-0.25,-0.25){\bf{B}}\put(1.18,2.6){\bf{A}}\put(2.55,-0.25){\bf{C}}\put(1.18,-0.25){\bf{D}}\qbezier(0.9,2.5)(0.8,2.3)(1.07,2.15)\qbezier(1.6,2.5)(1.67,2.2)(1.45,2.15)\put(0.6,2.1){$\bf x^{\circ}$}\put(1.7,2.1){$\bf y^{\circ}$}\qbezier(0.17,0.3)(0.37,0.3)(0.4,0)\qbezier(2.06,0)(2.2,0.3)(2.35,0.3)\put(0.5,0.3){$\bf x^{\circ}$}\put(1.87,0.27){$\bf y^{\circ}$}\end{picture}
- Integrals :
\boxed{\boxed{\begin{minipage}{4cm}\displaystyle\circ\sf\:\int{1\:dx}=x+c\\\\\circ\sf\:\int{a\:dx}=ax+c\\\\\circ\sf\:\int{x^n\:dx}=\dfrac{x^{n+1}}{n+1}+c\\\\\circ\sf\:\int{sin\:x\:dx}=-cos\:x+c\\\\\circ\sf\:\int{cos\:x\:dx}=sin\:x+c\\\\\circ\sf\:\int{sec^2x\:dx}=tan\:x+c\\\\\circ\sf\:\int{e^x\:dx}=e^x+c\end{minipage}}}
- Rectangle related :
\setlength{\unitlength}{1.2cm}\begin{picture}(0,0)\thicklines\put(0.6,0.9){\sf C}\put(4.17,0.9){\sf D}\put(4.17,3){\sf B}\put(0.6,3){\sf A}\qbezier(1,1)(1,1)(4,1)\qbezier(4,1)(4,1)(4,3)\qbezier(4,3)(4,3)(1,3)\qbezier(1,3)(1,3)(1,1)\qbezier(1,3)(1,3)(4,1)\put(5,2){\sf\large =}\qbezier(6,1)(6,1)(6,3)\qbezier(6,3)(6,3)(9,1)\qbezier(9,1)(9,1)(6,1)\put(5.8,3.1){\sf A}\put(5.55,0.85){\sf C}\put(9.2,0.8){\sf D}\put(9,2){\sf\large +}\qbezier(10,3)(10,3)(13,3)\qbezier(13,3)(13,3)(13,1)\qbezier(13,1)(13,1)(10,3)\put(12.8,0.5){\sf D}\put(13.1,3.1){\sf B}\put(9.8,3.1){\sf A}\end{picture}
- Sphere :
\setlength{\unitlength}{1.2cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\qbezier(-2.3,0)(0,-1)(2.3,0)\qbezier(-2.3,0)(0,1)(2.3,0)\thinlines\qbezier (0,0)(0,0)(0.2,0.3)\qbezier (0.3,0.4)(0.3,0.4)(0.5,0.7)\qbezier (0.6,0.8)(0.6,0.8)(0.8,1.1)\qbezier (0.9,1.2)(0.9,1.2)(1.1,1.5)\qbezier (1.2,1.6)(1.2,1.6)(1.38,1.9)\put(0.2,1){\bf R}\end{picture}
- Natural logarithm :
\boxed{\boxed{\begin{minipage}{4.2cm}\circ\sf\:\ln 1=0\\\circ\sf\:\ln e=1\\\circ\sf\:\ln x=y\leftrightarrow e^y=x\\\circ\sf\:e^{\ln x}=x,\:x>0\\\circ\sf\:\ln(e^x)=x,\:x\in\mathbb{\large R}\\\circ\sf\:\ln(xy)=\ln x+\ln y\\\circ\sf\:\ln(x/y)=\ln x-\ln y\\\circ\sf\:\ln(x^r)=r\ln x\\\circ\sf\:\ln x=log_e\:x\end{minipage}}}
- Obtuse angle :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\linethickness{.4mm}\qbezier(1,1)(1,1)(5.5,1)\qbezier(1,1)(1,1)( -1,4)\qbezier(0.65,1.55)(1.5,1.8)(2,1)\put(3,3){\bf Obtuse Angle :}\put(3,2.5){\sf measures more than}\put(3,2){\sf 90 degrees}\end{picture}
- Profit and loss :
\boxed{\begin{minipage}{5cm}\bigstar$\:\underline{\textbf{Profit and Loss Formulas :}}\\\\ \\ \sf {\textcircled{\footnotesize\textsf{1}}} \:S.P. =$\sf \bigg\lgroup\dfrac{100 + Profit \%}{100}\bigg\rgroup \times 100$\\\\\\ \sf {\textcircled{\footnotesize\textsf{2}}} \:\:C.P. = $\sf \dfrac{S.P. \times 100}{100 + Profit \%}$\\\\\\\sf{\textcircled{\footnotesize\textsf{3}}} \:\:Profit = $\sf \dfrac{Profit \% \times C.P.}{100}$\\\\\\ \sf{\textcircled{\footnotesize\textsf{4}}} \: \:Profit (gain) = S.P. - C.P. \\\\\\\sf{\textcircled{\footnotesize\textsf{5}}} \: \:$\sf Profit \% = \dfrac{Profit}{C.P.} \times 100$\end{minipage}}
- Formulas (Cylinder) :
\boxed{\begin{minipage}{6.2 cm}\bigstar$\:\underline{\textbf{Formulae Related to Cylinder :}}\\\\\sf {\textcircled{\footnotesize\textsf{1}}} \:Area\:of\:Base\:and\:top =\pi r^2 \\\\ \sf {\textcircled{\footnotesize\textsf{2}}} \:\:Curved \: Surface \: Area =2 \pi rh\\\\\sf{\textcircled{\footnotesize\textsf{3}}} \:\:Total \: Surface \: Area = 2 \pi r(h + r)\\ \\{\textcircled{\footnotesize\textsf{4}}} \: \:Volume=\pi r^2h\end{minipage}}
- Median :
\boxed{\begin{minipage}{6cm}$\bigstar$\:\:\sf Median = l + $\sf\dfrac{\frac{n}{2}-C.f.}{f}\times h\\\\Here: \\1)\:n = \sum f =\\2)\:l=Lower\:limit\:of\:median\:class=\\3)\:C.f.=Cumulative\:frequency\:of\:class\\preceeding\:the\:median\:class=\\4)\:f= frequency\:of\:median\:class=\\5)\:h= Class\:interval = \end{minipage}}
- Right angle :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\linethickness{.4mm}\put(1,1){\line(1,0){4.5}}\put(1,1){\line(0,1){3.5}}\put(1.02,1.02){\framebox(0.3,0.3)}\put(3,3.5){\bf Right Angle :}\put(3,3){\sf measures exactly}\put(3,2.5){\sf 90 degrees}\end{picture}
- The CAST diagram :
\setlength{\unitlength}{7mm}\begin{picture}(0,0)\thicklines\put(0,0){\vector(1,0){6}}\put(0,0){\vector(-1,0){6}}\put(0,0){\vector(0,1){6}}\put(0,0){\vector(0,-1){6}}\put( -3,4){\sf\huge S}\put(3,4){\sf\huge A}\put( -3, - 2){\sf\huge T}\put(3, - 2){\sf\huge C}\put( -4.5,2.5){\sf\large Sin is positive}\put(1.5,2.5){\sf\large All are positive}\put( -4.5, - 3){\sf\large Tan is positive}\put(2, - 3){\sf\large Cos is positive}\put( -4.1,1.5){\sf Cos and Tan }\put( -4.1,1){\sf are negative}\put( -4.1, -4){\sf Sin and Cos}\put( -4.1, - 4.5){\sf are negative}\put(2.4, - 4){\sf Sin and Tan}\put(2.4, - 4.5){\sf are negative}\end{picture}
- Diff. Formulas (Trigonometry) :
\boxed{\boxed{\begin{minipage}{5cm}\displaystyle\circ\sf\;\dfrac{d}{dx}(sin\;x)=cosx \\\\ \circ \;\dfrac{d}{dx}(cos\;x) = -sinx \\\\ \circ \; \dfrac{d}{dx}(tan\;x) = sec^{2}x \\\\ \circ\; \dfrac{d}{dx}(cot\;x) = -csc^{2}x \\\\ \circ \; \dfrac{d}{dx}(sec\;x) = secx \cdot tanx \\\\ \circ \; \dfrac{d}{dx}(csc\;x) = -cscx \cdot cotx \\\\ \circ\; \dfrac{d}{dx}(sinh\;x)=coshx \\\\ \circ\; \dfrac{d}{dx}(cosh\;x)= sinhx \\\\ \circ\;\dfrac{d}{dx}(tanh\;x)=sech^{2}h \\\\ \circ\;\dfrac{d}{dx}(coth\;x)=-csch^{2}x \\\\ \circ\;\dfrac{d}{dx}(sech\;x) =-sechx \cdot tanhx \\\\ \circ\;\dfrac{d}{dx}(csch\;x) = -cschx \cdot cothx\end{minipage}}}
- Interior angles (C) :
- Alternate angles (Z) :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\multiput(0,0)(0,3){2}{\line(1,0){4}}\qbezier(0,0)(0,0)(4,3)\qbezier(1,0)(1.2,0.35)(0.8,0.6)\qbezier(3,3)(2.8,2.65)(3.2,2.4)\put(2.5,0.02){\vector(1,0){0}}\put(1.5,3.02){\vector(-1,0){0}}\end{picture}
- Logarithm equations :
\boxed{\boxed{\begin{minipage}{5cm}\displaystyle\circ\sf\ ^{a} log \ a= 1\\\\\circ \ ^{a}log \ 1 = 0 \\\\\circ \ ^{a ^{n}} log \ b^{m}= \dfrac{m}{n} \times\:^{a}log \ b \\\\\circ \ ^{a^{m}} \ log \ b^{m} = \ ^{a}log \ b \\\\\circ \ ^{a}log \ b = \dfrac{1}{^{b}log \ a} \\\\\circ \ ^{a}log \ b = \dfrac{^{m}log \ b}{^{m} log \ a} \\\\\circ \ a^{^{a} logb} = b \\\\\circ \ ^{a}log \ b + ^{a}log \ c = \ ^{a}log(bc) \\\\\circ \ ^{a}log \ b -\: ^{a}log \ c = \ ^{a}log \left( \dfrac{b}{c} \right) \\\circ \ ^{a}log \ b \:\cdot\: ^{a}log \ c = \ ^{a}log \ c \\\\\circ \ ^{a}log \left( \dfrac{b}{c} \right) = \ ^{a}log \left(\dfrac{c}{b}\right)\end{minipage}}}
- Linear Pair :
\setlength{\unitlength}{1 cm}\begin{picture}(0,0)\thicklines\put(5,1){\vector(1,0){4}}\put(5,1){\vector(-1,0){4}}\put(5,1){\vector(1,1){3}}\put(2,2){$\underline{\boxed{\large\sf a + b = 180^{\circ}}$}}\put(4.5,1.3){$\sf a^{\circ}$}\put(5.7,1.3){$\sf b^{\circ}$}\end{picture}
- Corresponding angles (F) :
- Acute angle :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\linethickness{.4mm}\qbezier(1,1)(1,1)(5.5,1)\qbezier(1,1)(1,1)(5,4)\qbezier(1.7,1.55)(2.2,1.3)(2,1)\put(5,3){\bf Acute Angle :}\put(4.9,2.5){\sf measures less than}\put(5,2){\sf 90 degrees}\end{picture}
- Formulas (Cone) :
\boxed{\begin{minipage}{6 cm}\bigstar$\:\underline{\textbf{Formulae Related to Cone :}}\\\\\sf {\textcircled{\footnotesize\textsf{1}}} \:Area\:of\:Base =\pi r^2 \\\\ \sf {\textcircled{\footnotesize\textsf{2}}} \:\:Curved \: Surface \: Area = \pi rl\\\\\sf{\textcircled{\footnotesize\textsf{3}}} \:\:TSA = Area\:of\:Base + CSA=\pi r^2+\pi rl\\ \\{\textcircled{\footnotesize\textsf{4}}} \: \:Volume=\dfrac{1}{3}\pi r^2h\\ \\{\textcircled{\footnotesize\textsf{5}}} \: \:Slant \: Height=\sqrt{r^2 + h^2}\end{minipage}}
- Anchor chart on real numbers :
\setlength{\unitlength}{15mm}\begin{picture}(10,10)\thicklines \put(0,8){\framebox{\framebox{\large{\bf{Natural}}}}}\put(0.6,7.3){\huge{$\downarrow$}} \put(0.1,6.6){\framebox{\framebox{\large{\bf{Whole}}}}}\put(0.6,5.9){\huge{$\downarrow$}} \put(0.05,5.15){\framebox{\framebox{\large{\bf{Integer}}}}} \put(0.6,4.3){\huge{$\downarrow$}}\put(-0.05,3.5){\framebox{\framebox{\large{\bf{Rational}}}}}\put(2.8,3.5){\framebox{\framebox{\large{\bf{Irrational}}}}}\put(0.6,2.7){\huge{$\downarrow$}}\put(3.5,2.7){\huge{$\downarrow$}}\put(-0.3,1.8){\framebox{\framebox{\huge{\bf{\quad Real\:numbers\quad}}}}}\end{picture}
- Distance and height :
\setlength{\unitlength}{15mm}\begin{picture}(8,8)\thicklines\put(0,0){\line(1,0){4}}\put(4,0){\line(0,1){1.65}}\put(4,2.13){\line(0,1){1.44 }}\qbezier(0,0)(2,1.9)(3.77,3.8)\qbezier(0,0)(1,0.45)(3.77,1.9) \put(3.7,0){\line(0,1){0.3}}\put(3.7,0.3){\line(1,0){0.3}}\qbezier(0.6,0)(0.6,0.4)(0.4,0.4)\qbezier(0.8,0)(0.8,0.2)(0.7,0.33)\put(0.9,0.2){$30^{\circ}$}\put(0.8,0.6){$60^{\circ}$} \put(2,-0.3){\bf{x}}\put(4,1.9){\circle{0.5}} \put(4,3.8){\circle{0.5}}\put(4.2,1){$\bf{h_1}$} \put(4.2,2.8){$\bf{h_2}$}\end{picture}
- Formulas of area :
\boxed{\begin {minipage}{9cm}\\ \dag\quad \Large\underline{\bf Formulas\:of\:Areas:-}\\ \\ \star\sf Square=(side)^2\\ \\ \star\sf Rectangle=Length\times Breadth \\\\ \star\sf Triangle=\dfrac{1}{2}\times Breadth\times Height \\\\ \star \sf Scalene\triangle=\sqrt {s (s-a)(s-b)(s-c)}\\ \\ \star \sf Rhombus =\dfrac {1}{2}\times d_1\times d_2 \\\\ \star\sf Rhombus =\:\dfrac {1}{2}p\sqrt {4a^2-p^2}\\ \\ \star\sf Parallelogram =Breadth\times Height\\\\ \star\sf Trapezium =\dfrac {1}{2}(a+b)\times Height \\ \\ \star\sf Equilateral\:Triangle=\dfrac {\sqrt{3}}{4}(side)^2\end {minipage}}
- Rectangle with diagonals :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\qbezier (0,0)(0,0)(5,0)\qbezier (0,0)(0,0)(0,3)\qbezier (0,3)(0,3)(5,3)\qbezier (5,3)(5,3)(5,0)\qbezier (0,3)(5,0)(5,0)\qbezier (0,0)(0,0)(5,3)\put (-0.4,-0.2){\sf D}\put (-0.2,3.1){\sf A}\put (5.2,3.1){\sf B}\put (5.2,-0.2){\sf C}\put (2.4,1){\sf O}\put (2,-0.4){\bf x\:cm}\put (-1,1.5){\sf y\:cm}\end {picture}
- Cylinder inside hollow cylinder :
\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\multiput(0,0)(4,0){2}{\line(0,1){6}}\multiput(1,0)(2,0){2}{\line(0,1){6}}\multiput(0,0)(0,6){2}{\qbezier(0,0)(2,-0.6)(4,0)}\multiput(0,0)(0,6){2}{\qbezier(0,0)(2,0.6)(4,0)}\multiput(1,0)(0,6){2}{\qbezier(0,0)(1,-0.2)(2,0)}\multiput(1,0)(0,6){2}{\qbezier(0,0)(1,0.2)(2,0)}\multiput(2,0.07)(0,0.3){20}{\line(0,1){0.2}}\multiput(2,4)(0.3,0){7}{\line(1,0){0.2}}\multiput(2,2)(-0.27,0){4}{\line(-1,0){0.2}}\put(1.4,1.5){\bf\large r}\put(3.35,3.45){\bf R}\put(1.4,3){\bf H}\end{picture}